0%

leetcode每日一题-缺失的第一个正数

Posted on Edited on In ,

缺失的第一个正数

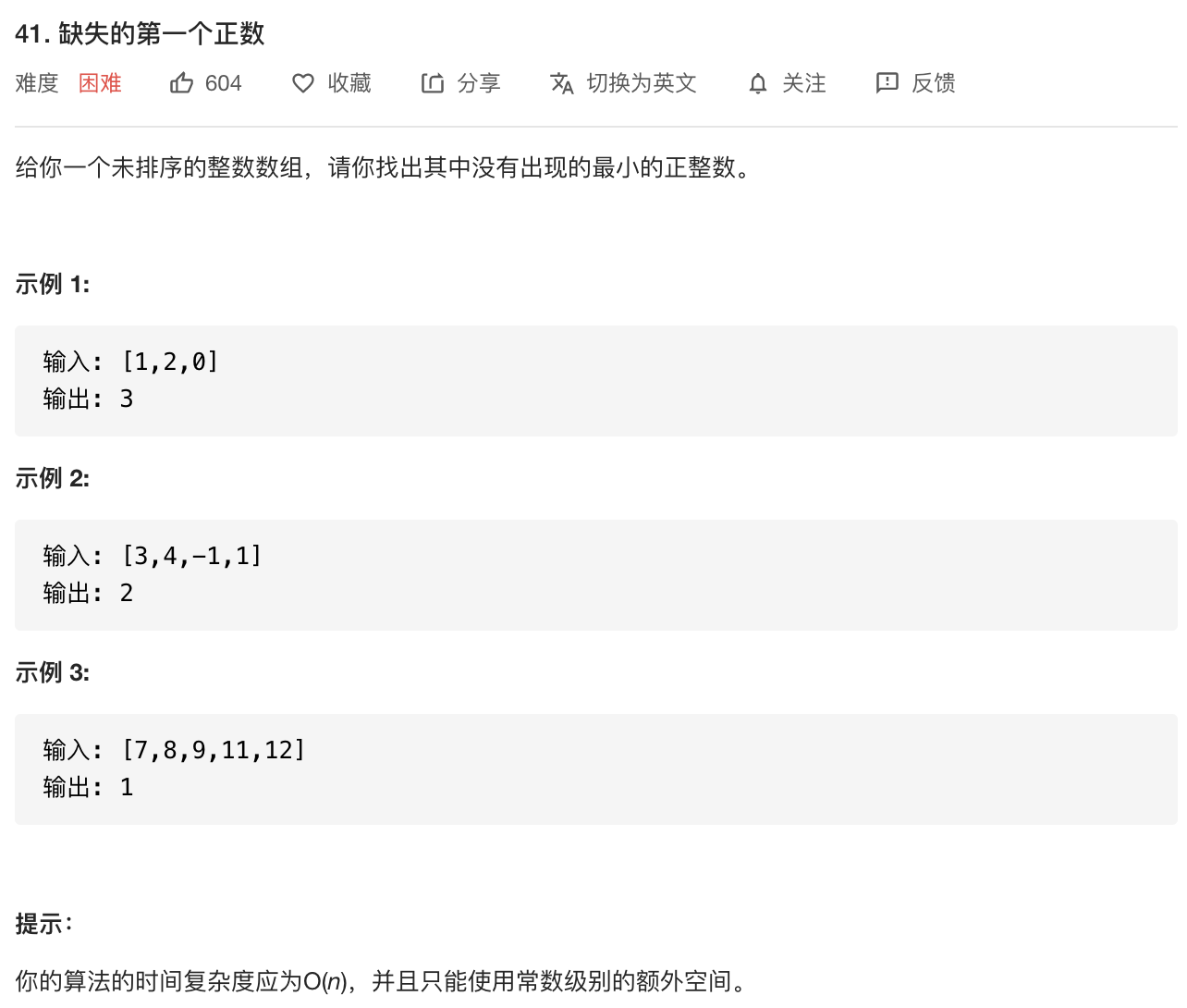
image1

这题只想出来了时间复杂度$O(N)$，空间复杂度$O(N)$的做法，思路就是把数组所有的数都存入哈希表，随后从1 开始依次枚举正整数，并判断其是否在哈希表中。代码如下：

1
class Solution {
2
    public int firstMissingPositive(int[] nums) {
3
        Set<Integer> set = new HashSet<>();
4
        int len = nums.length;
5
        for(int i=0; i<len; i++){
6
            set.add(nums[i]);
7
        }
8
        for(int i=1; i<=len; i++){
9
            if(!set.contains(i)){
10
                return i;
11
            }
12
        }
13
        return len+1;
14
    }
15
}

但是题目要求空间复杂度为$O(1)$，即不能使用额外的存储空间，但没有限制不能对原数组进行修改，因此可以利用原数组来满足空间复杂度要求。

方法一：哈希表

对于一个长度为$N$的数组，其中没有出现的最小正整数只能在$[1,N+1]$中。这是因为如果$[1,N]$都出现了，那么答案一定是$N+1$，否则答案就是$[1,N]$中没有出现的最小正整数。在上面的方法中，我们将所有在范围内的数放入哈希表，可以得到最终的答案。但是这里不能申请额外空间，而给定的数组恰好长度为$N$，因此可以利用给定的数组设计成类似哈希表的东西。

我们可以遍历数组，对于遍历到的数$x$，如果不在$[1,N]$范围内就忽略。否则，就将数组第$x-1$个位置打上标记，表明该数出现过（数组下标从0开始，因此数组下标$x-1$代表的数为$x$）。在遍历结束之后，如果所有的位置都被打上标记，那么答案就是$N+1$，否则答案是最小的没有打上标记的位置加1。

由于数组中可能出现负数，因此需要先遍历数组，将负数变为无关紧要的数，例如$N+1$，同时这里标记可以使用负号。算法流程如下：

  • 先将数组中所有小于等于0的数变为$N+1$。
  • 遍历数组中的每一个数$x$，如果对应位置$|x|-1$已经打上标记（使用绝对值是因为$x$如果已经标记过那么它现在为负数），那么就跳过，否则就打上标记。
  • 在遍历完成后，如果数组每一个位置都为负数，那么答案为$N+1$，否则为第一个正数出现的位置加1。
1
class Solution {
2
    public int firstMissingPositive(int[] nums) {
3
        int len = nums.length;
4
        for(int i=0; i<len; i++){
5
            if(nums[i] <= 0){
6
                nums[i] = len+1;
7
            }
8
        }
9
        for(int i=0; i<len; i++){
10
            int num = Math.abs(nums[i]);
11
            if(num<=len && num>=1){
12
                nums[num-1] = -Math.abs(nums[num-1]);
13
            }
14
        }
15
        for(int i=0; i<len; i++){
16
            if(nums[i] > 0){
17
                return i+1;
18
            }
19
        }
20
        return len+1;
21
    }
22
}

复杂度分析

  • 时间复杂度：$O(N)$
  • 空间复杂度：$O(1)$

方法二：置换

基本思想就是将数组恢复成下面的形式：

如果数组中包含$x \in [1,N]$，那么将数组的第$x-1$个位置的元素恢复为$x$。

在恢复之后，数组的形式应该为$[1,2,…,N]$的形式，但其中有若干个位置错误，每一个错误的位置就代表了一个缺失的正数。我们可以对数组进行一次遍历，对于遍历到的数$x=nums[i]$，如果$x \in [1,N]$，那么$nums[i]$和$nums[x-1]$就交换位置，新交换得到的$nums[i]$可能仍在$[1,N]$范围内，此时继续交换，直到$x \notin [1,N]$。

1
class Solution {
2
    public int firstMissingPositive(int[] nums) {
3
        int len = nums.length;
4
        for(int i=0; i<len; i++){
5
            //进入置换,其中nums[nums[i]-1] != nums[i]防止陷入死循环
6
            while(nums[i]>=1 && nums[i]<=len && nums[nums[i]-1] != nums[i]){
7
                int temp = nums[nums[i]-1];
8
                nums[nums[i]-1] = nums[i];
9
                nums[i] = temp;
10
            }
11
        }
12
        for(int i=0; i<len; i++){
13
            if(nums[i] != i+1){
14
                return i+1;
15
            }
16
        }
17
        return len+1;
18
    }
19
}

复杂度分析

  • 时间复杂度：$O(N)$

  • 空间复杂度：$O(1)$