0%

leetcode每日一题-长度最小的子数组

Posted on Edited on In ,

长度最小的子数组

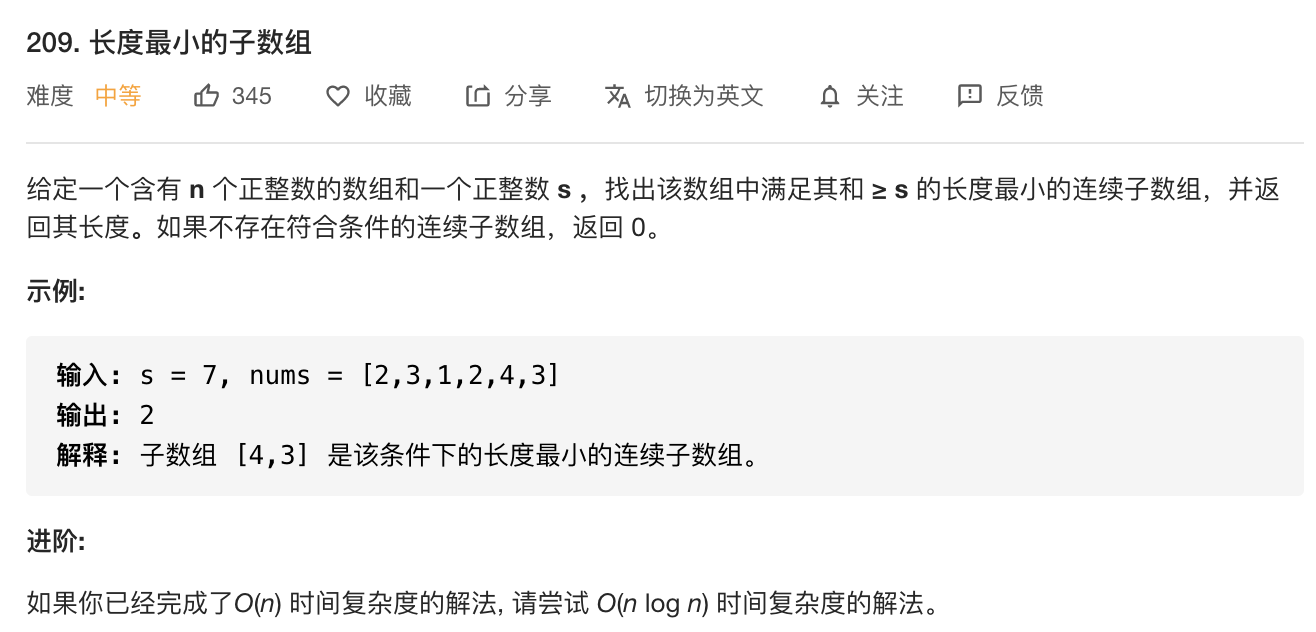
image1

可以使用双指针解决此问题。定义两个指针$left$和$right$，分别表示子数组的左边界和右边界，维护变量$sum$存储子数组中的元素和（即从$nums[left]$到$nums[right]$的元素和）。

初始状态下，$left$和$right$都指向下标0，$sum$的值也为0。每一轮迭代，将$nums[right]$加到$sum$，如果$sum$的值$>=s$，则更新子数组的最小长度，此时子数组的长度为$right-left+1$，然后将左指针$left$右移，即将$nums[left]$从$sum$中减去，直到$sum<s$，在此过程中同样更新子数组最小长度，在每一轮迭代之后，将右指针$right$右移。

1
class Solution {
2
    public int minSubArrayLen(int s, int[] nums) {
3
        int n = nums.length;
4
        if(n == 0){
5
            return 0;
6
        }
7
        int sum = 0;
8
        int left=0, right=0;
9
        int ans = n+1;
10
        while(right < n){
11
            sum += nums[right];
12
            while(sum >= s && left<=right){
13
                ans = Math.min(ans, right-left+1);
14
                sum = sum - nums[left];
15
                left++;
16
            }
17
            right++;
18
        }
19
        return ans==n+1 ? 0 : ans;
20
    }
21
}

复杂度分析

  • 时间复杂度：$O(N)$
  • 空间复杂度：$O(1)$

##进阶

如果使用暴力法，即两次循环那么时间复杂度为$O(n^2)$。如果将第二层循环替代为二分查找，那么就可以将时间复杂度降为$O(nlogn)$。为了使用二分查找，需要额外创建一个数组 sums 用于存储数组 nums 的前缀和，其中$sums[i]$表示从$nums[0]$到$nums[i-1]$的和。得到前缀和之后，对于每个开始下标$i$，可通过二分查找得到大于或等于$i$ 的最小下标 $bound$ ，使得$sums[bound]-sums[i-1]>=s$， 并更新子数组的最小长度，此时长度为$bound-(i-1)$。

1
class Solution {
2
    public int minSubArrayLen(int s, int[] nums) {
3
        int n = nums.length;
4
        if (n == 0) {
5
            return 0;
6
        }
7
        int ans = n+1;
8
        int[] sums = new int[n + 1]; 
9
        // 为了方便计算，令 size = n + 1 
10
        // sums[0] = 0 意味着前 0 个元素的前缀和为 0
11
        // sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
12
        // 以此类推
13
        for (int i = 1; i <= n; i++) {
14
            sums[i] = sums[i - 1] + nums[i - 1];
15
        }
16
        for (int i = 1; i <= n; i++) {
17
            int target = s + sums[i - 1];
18
            int bound = Arrays.binarySearch(sums, target);
19
            if (bound < 0) {
20
                bound = -bound - 1;
21
            }
22
            if (bound <= n) {
23
                ans = Math.min(ans, bound - (i - 1));
24
            }
25
        }
26
        return ans == n+1 ? 0 : ans;
27
    }
28
}

复杂度分析

  • 时间复杂度：$O(nlogn)$
  • 空间复杂度：$O(n)$