0%

leetcode每日一题-用两个栈实现队列

Posted on Edited on In ,

用两个栈实现队列

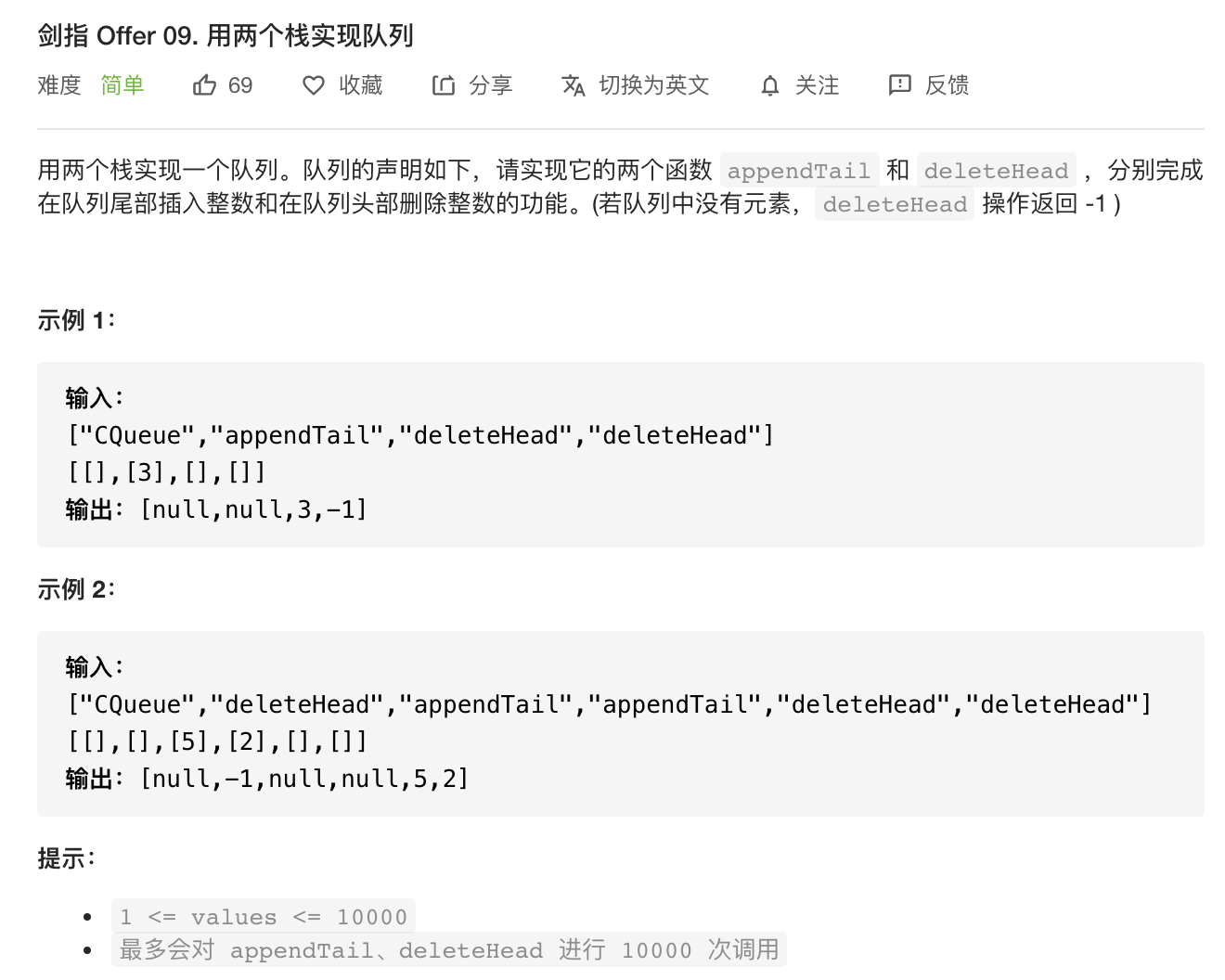
image1

栈初始化和调用方式如下：

1
/**
2
 * Your CQueue object will be instantiated and called as such:
3
 * CQueue obj = new CQueue();
4
 * obj.appendTail(value);
5
 * int param_2 = obj.deleteHead();
6
 */

基本思想就是一个栈$Stack1$只用来入队列，另一个栈$Stack2$只用来出队列。当$Stack2$出队列时就弹栈，但栈为空时，就将$Stack1$中的数都弹栈并压入$Stack2$中，此时第二个栈中元素的顺序就是待删除的元素的顺序。代码如下：

1
class CQueue {
2
    Stack<Integer> stack1;
3
    Stack<Integer> stack2;
4
5
    public CQueue() {
6
        stack1 = new Stack<Integer>();
7
        stack2 = new Stack<Integer>();
8
    }
9
    
10
    public void appendTail(int value) {
11
        stack1.push(value);
12
    }
13
    
14
    public int deleteHead() {
15
        if(!stack2.empty()){
16
            return stack2.pop();
17
        }else{
18
            if(stack1.empty()){
19
                return -1;
20
            }else{
21
                while(!stack1.empty()){
22
                    stack2.push(stack1.pop());
23
                }
24
                return stack2.pop();
25
            }
26
        }
27
    }
28
}

复杂度分析

  • 时间复杂度：$O(1)$。使用均摊分析可以得到。
  • 空间复杂度：$O(n)$。