0%

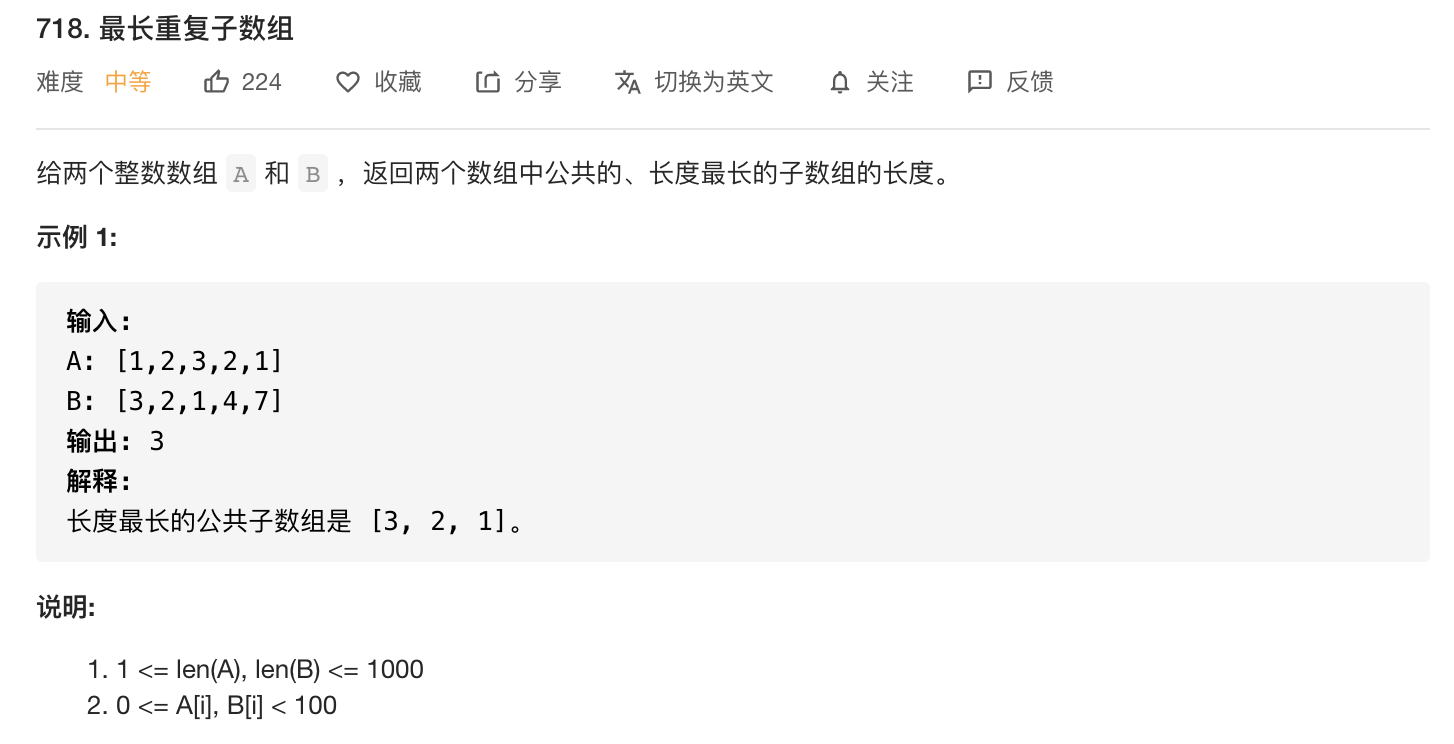
leetcode每日一题-最长重复子数组

Posted on Edited on In ,

最长重复子数组

image1

方法一：动态规划

令dp[i][j]表示A[i:]和B[j:]的最长公共前缀，如果A[i]==B[j]，那么dp[i][j] = dp[i+1][j+1]+1，否则dp[i][j]=0。最后的结果就为所有dp[i][j]中的最大值。

1
class Solution {
2
    public int findLength(int[] A, int[] B) {
3
        int m = A.length;
4
        int n = B.length;
5
        int[][] dp = new int[m+1][n+1];
6
        int ans = 0;
7
        for(int i=m-1; i>=0; i--){
8
            for(int j=n-1; j>=0; j--){
9
                if(A[i] == B[j]){
10
                    dp[i][j] = dp[i+1][j+1]+1;
11
                }else{
12
                    dp[i][j] = 0;
13
                }
14
                ans = Math.max(ans, dp[i][j]);
15
            }  
16
        } 
17
        return ans;
18
    }
19
}

复杂度分析：

  • 时间复杂度：$O(M \times N)$。其中$M$为数组A的长度，$N$为数组B的长度。
  • 空间复杂度：$O(M \times N)$。

方法二：滑动窗口

枚举所有A和B的对齐方式，对齐的方式有两种：第一种是固定数组B，枚举数组A的任意一个数A[i]作为头部与数组B的头部B[0]对齐并计算重复子数组长度。第二种是固定数组A，进行同样操作。

1
class Solution {
2
    public int findLength(int[] A, int[] B) {
3
        int m = A.length;
4
        int n = B.length;
5
        int ans = 0;
6
        for(int i=0; i<m; i++){
7
            int len = Math.min(m-i, n);
8
            int maxlen = maxLength(A, B, i, 0, len);
9
            ans = Math.max(ans, maxlen);
10
        }
11
        for(int i=0; i<n; i++){
12
            int len = Math.min(m, n-i);
13
            int maxlen = maxLength(A, B, 0, i, len);
14
            ans = Math.max(ans, maxlen);
15
        }
16
        return ans;
17
    }
18
19
    public int maxLength(int[] A, int[] B, int addA, int addB, int len){
20
        int k=0, ret=0;
21
        for(int i=0; i<len; i++){
22
            if(A[addA+i] == B[addB+i]){
23
                k++;
24
            }else{
25
                k = 0;
26
            }
27
            ret = Math.max(ret, k);
28
        }
29
        return ret;
30
    }
31
}

复杂度分析

  • 时间复杂度：$O((M+N) \times min(M,N))$。
  • 空间复杂度：$O(1)$。