0%

leetcode每日一题-有序矩阵中第K小的元素

Posted on Edited on In ,

有序矩阵中第K小的元素

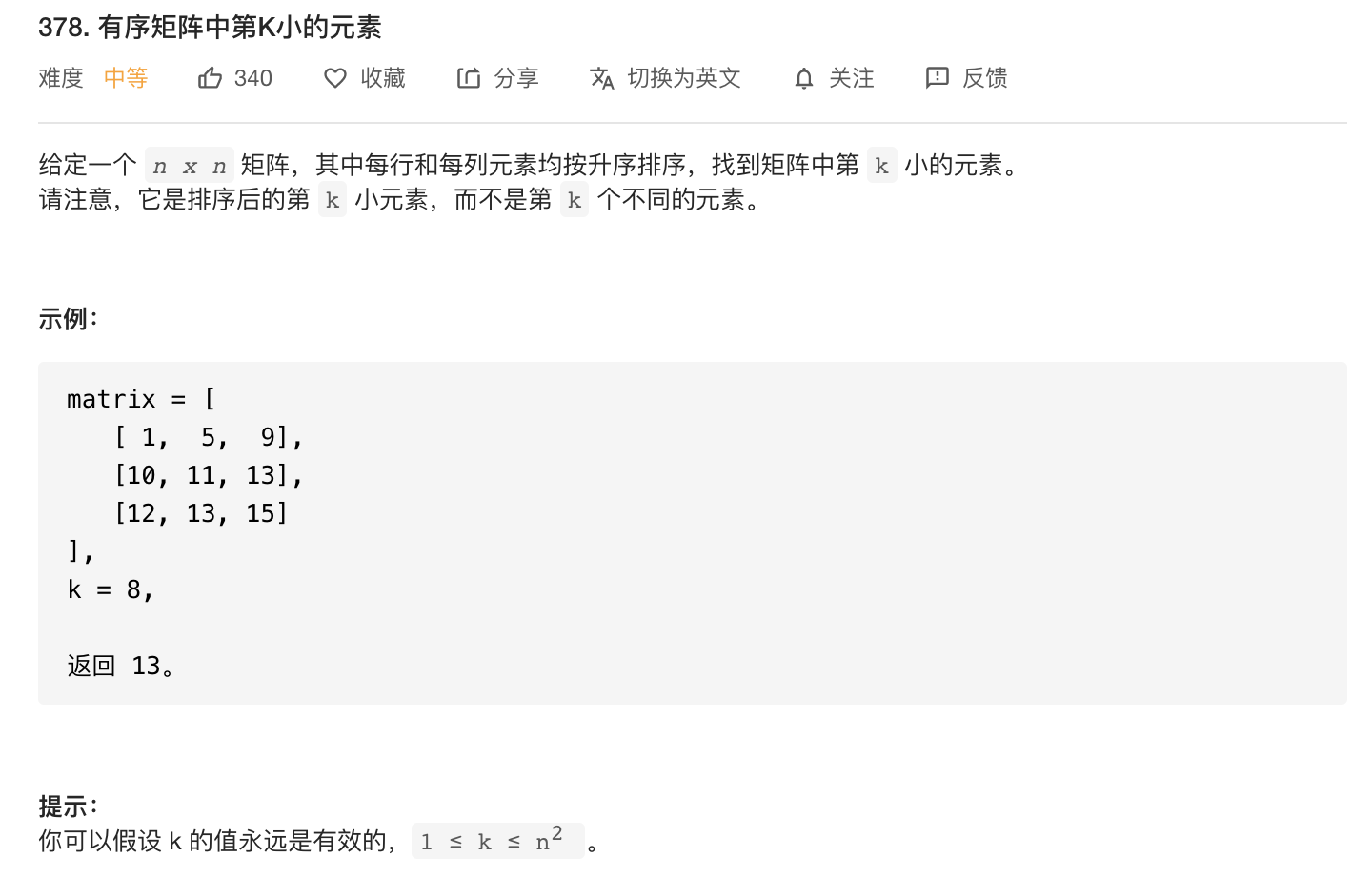
image1

方法一：暴力法

将矩阵中的元素存入一维数组，然后进行排序，返回下标为k-1的数。

1
class Solution {
2
    public int kthSmallest(int[][] matrix, int k) {
3
        // 暴力算法
4
        int rows = matrix.length, columns = matrix[0].length;
5
        int[] sorted = new int[rows * columns];
6
        int index = 0;
7
        for (int[] row : matrix) {
8
            for (int num : row) {
9
               sorted[index++] = num;
10
            }
11
        }
12
        Arrays.sort(sorted);
13
        return sorted[k - 1];
14
    }
15
}

复杂度分析：

  • 时间复杂度：$O(n^2logn)$。
  • 空间复杂度：$O(n^2)$。

方法二：小根堆

思路同topK问题，先将第一列的数存入小根堆，之后进行k-1次循环，每一次循环都删除堆顶并插入堆顶后的一个数，k-1次循环后，堆顶的元素就为第k小的元素。

1
class Solution {
2
		public int kthSmallest(int[][] matrix, int k) {
3
        // 堆排序
4
        int n = matrix.length;
5
        PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[0] - o2[0]);
6
        for(int i=0; i<n; i++){
7
            // 保存当前元素、行、列
8
            pq.offer(new int[]{matrix[i][0], i, 0});
9
        }
10
        for(int i=0; i<k-1; i++){
11
            int[] cur = pq.poll();
12
            if(cur[2] < n-1){
13
                pq.offer(new int[]{matrix[cur[1]][cur[2]+1], cur[1], cur[2]+1});
14
            }
15
        }
16
        return pq.poll()[0];
17
		}
18
}

复杂度分析：

  • 时间复杂度：$O(klogn)$。k在最坏情况下为$n^2$。
  • 空间复杂度：$O(n)$。

方法三：二分查找

分析可知矩阵内的元素是从左上到右下递增的，其中最小的元素是$matrix[0][0]$，最大的元素是$matrix[n-1][n-1]$，分别记为$l$和$r$。

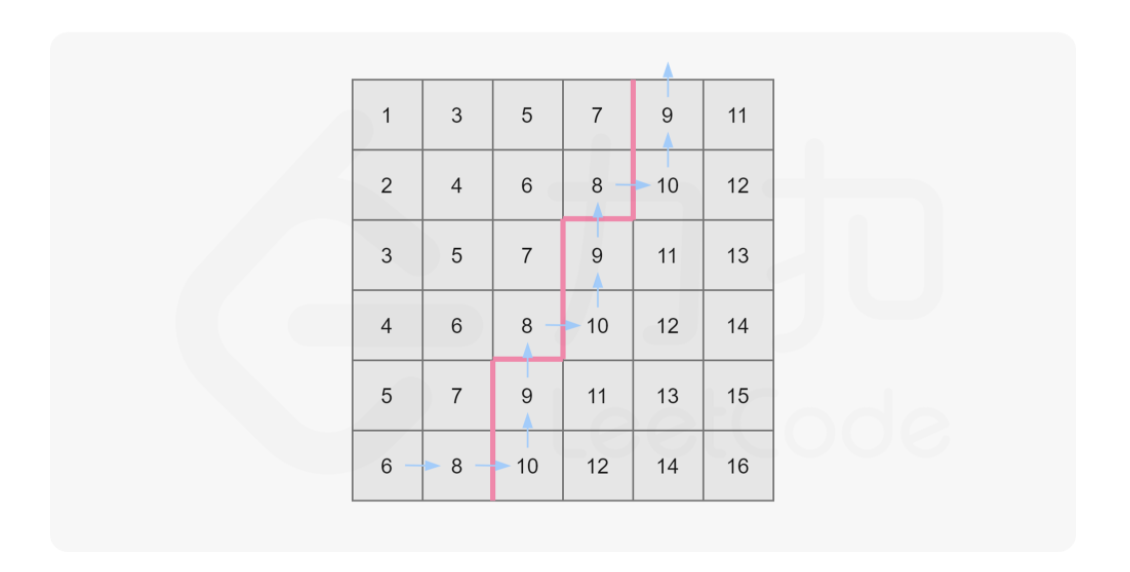
如果任取一个数$mid$满足$l<=mid<=r$，那么矩阵中不大于$mid$的数，肯定全分布在矩阵的左上角。我们可以从矩阵的左下角出发，统计出所有不大于$mid$的矩阵中数的数量。方法如下：

  • 初始位置在矩阵左下角$matrix[n-1][0]$
  • 设当前位置为$matrix[i][j]$，若$matrix[i][j]<=mid$，那么将当前列所在的不大于$mid$的数的数量（即$i+1$）累加到答案中，并向右移动，否则向上移动。
  • 不断移动直到走出矩阵。

如下图所示：

image2

1
class Solution {
2
    public int kthSmallest(int[][] matrix, int k) {
3
        int n = matrix.length;
4
        int left = matrix[0][0];
5
        int right = matrix[n - 1][n - 1];
6
        while (left <= right) {
7
            int mid = left + ((right - left) >> 1);
8
            if (check(matrix, mid, k, n)) {
9
                right = mid - 1;
10
            } else {
11
                left = mid + 1;
12
            }
13
        }
14
        return left;
15
    }
16
17
    public boolean check(int[][] matrix, int mid, int k, int n) {
18
        int i = n - 1;
19
        int j = 0;
20
        int num = 0;
21
        while (i >= 0 && j < n) {
22
            if (matrix[i][j] <= mid) {
23
                num += i + 1;
24
                j++;
25
            } else {
26
                i--;
27
            }
28
        }
29
        return num >= k;
30
    }
31
}

复杂度分析：

  • 时间复杂度：$O(nlog(r-l))$

  • 空间复杂度：$O(1)$