0%

leetcode每日一题-将有序数组转换为二叉搜索树

Posted on In ,

将有序数组转换为二叉搜索树

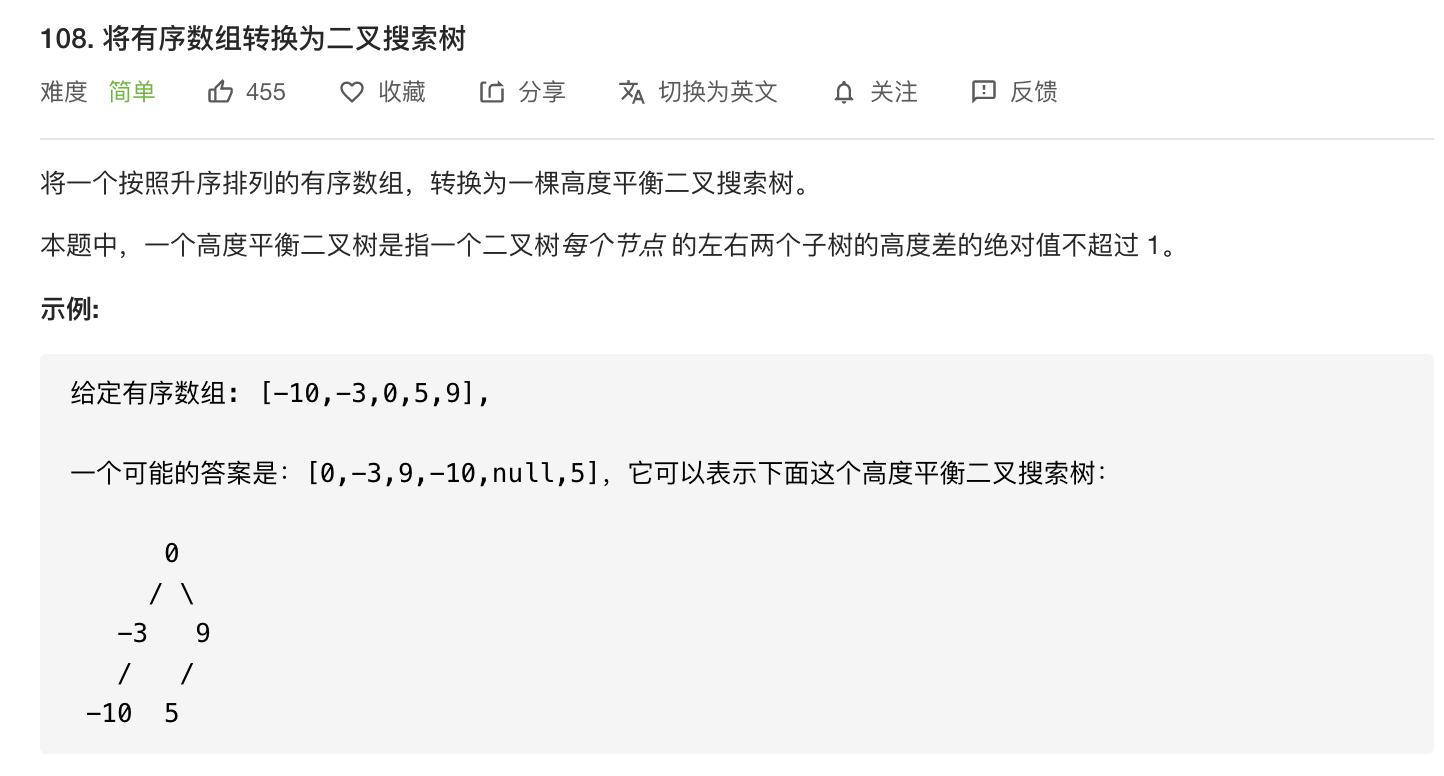
image1

树的结构为：

1
/**
2
 * Definition for a binary tree node.
3
 * public class TreeNode {
4
 *     int val;
5
 *     TreeNode left;
6
 *     TreeNode right;
7
 *     TreeNode(int x) { val = x; }
8
 * }
9
 */

使用递归的方式，每次取数组中间的数$mid$作为根节点，$mid$左边的递归构造左子树，$mid$右边的递归构造右子树。

1
class Solution {
2
    public TreeNode sortedArrayToBST(int[] nums) {
3
        if(nums==null || nums.length==0){
4
            return null;
5
        }
6
        return buildBST(nums, 0, nums.length-1);
7
    }
8
9
    public TreeNode buildBST(int[] nums, int start, int end){
10
        if(start > end){
11
            return null;
12
        }
13
        int mid = (start+end)/2;
14
        TreeNode node = new TreeNode(nums[mid]);
15
        node.left = buildBST(nums,start,mid-1);
16
        node.right = buildBST(nums,mid+1,end);
17
        return node;
18
    }
19
}

复杂度分析：

  • 时间复杂度：$O(n)$，数组中每个数字访问一次。
  • 空间复杂度：$O(logn)$，主要取决于递归栈的深度。