最佳买卖股票时机含冷冻期

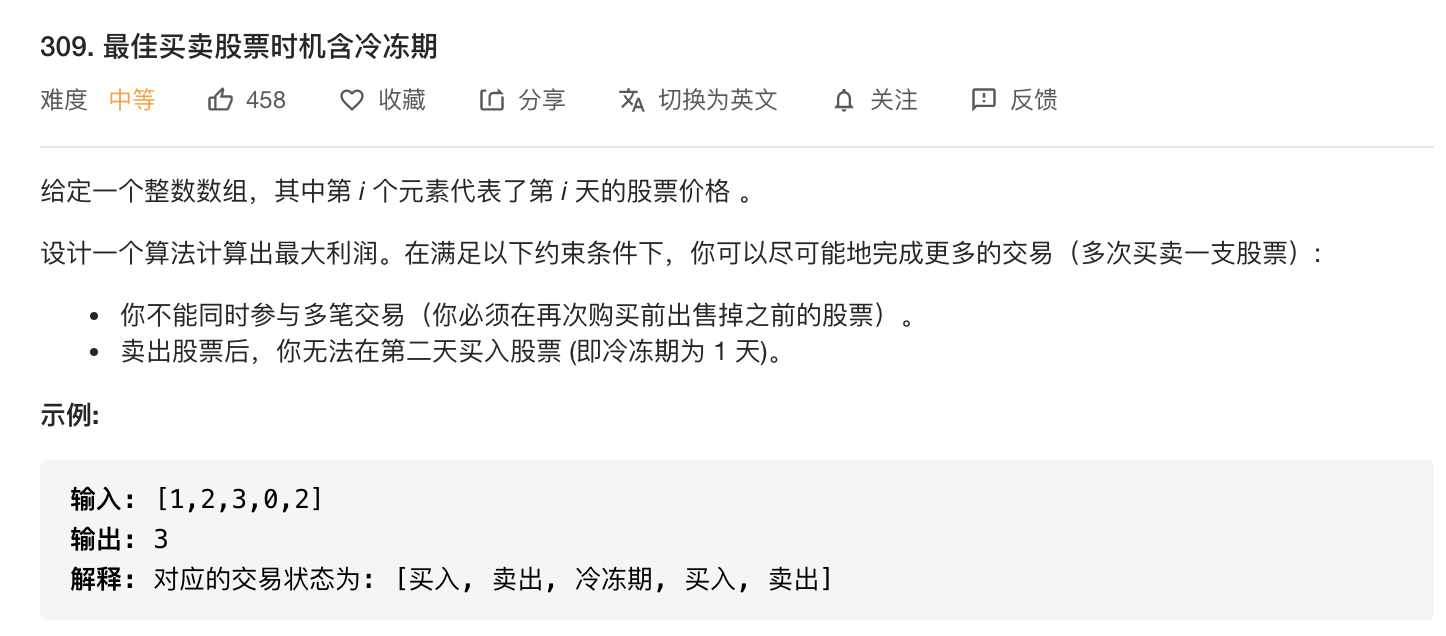
首先我们定义$dp[i]$表示第$i$天结束以后总的收益，因为含有冷冻期，所以我们定义三种状态：

$dp[i][0]$：第$i$天结束以后，持有一支股票，即当天进行买入操作或者第$i-1$天持有股票然后在第$i$天什么都没操作。
$dp[i][1]$：第$i$天结束以后，不持有股票，且进入冷冻期，即当天进行卖出操作。
$dp[i][2]$：第$i$天结束以后，不持有股票，也不进入冷冻期，即当天什么都没操作。

状态转移方程如下：

对于$dp[i][0]$，第$i$天的收益有两种情况，第一种是什么都没操作，第二种是当天进行买入操作。

$$
dp[i][0] = max(dp[i-1][0],dp[i-1][2]-prices[i])
$$

对于$dp[i][1]$，第$i$天的收益只有一种情况，就是卖出股票。

$$
dp[i][1] = dp[i-1][0]+prices[i]
$$

对于$dp[i][2]$，第$i$天的收益有两种情况，第一种是第$i-1$天就是第三种状态，且第$i$天什么都没操作，第二种是冷冻期结束。

$$
dp[i][2] = max(dp[i-1][1],dp[i-1][2])
$$

最后的结果应该是：
$$
max(dp[n-1][0],dp[n-1][1],dp[n-1][2])
$$
实际上不用比较$dp[n-1][0]$，应该如果在最后一天还持有股票，那么显然没有任何意义，所以只需要比较$dp[n-1][1]$和$dp[n-1][2]$就可以了。

第0天的情况为边界条件：

$dp[0][0] = -prices[0]$
$dp[0][1]=0$
$dp[0][2]=0$

1	/*
2	* @lc app=leetcode.cn id=309 lang=java
3	*
4	* [309] 最佳买卖股票时机含冷冻期
5	*/
6
7	// @lc code=start
8	class Solution {
9	public int maxProfit(int[] prices) {
10	if(prices.length == 0){
11	return 0;
12	}
13	int n = prices.length;
14	int[][] dp = new int[n][3];
15	dp[0][0] = -prices[0];
16	dp[0][1] = 0;
17	dp[0][2] = 0;
18	for(int i=1; i<n; i++){
19	dp[i][0] = Math.max(dp[i-1][0], dp[i-1][2]-prices[i]);
20	dp[i][1] = dp[i-1][0] + prices[i];
21	dp[i][2] = Math.max(dp[i-1][1], dp[i-1][2]);
22	}
23	return Math.max(dp[n-1][1], dp[n-1][2]);
24	}
25	}

复杂度分析：

时间复杂度：$O(n)$。
空间复杂度：$O(n)$。

注意到第$i$天的状态只与第$i-1$天的状态有关，可以由此进行空间的优化。

/*
 * @lc app=leetcode.cn id=309 lang=java
 *
 * [309] 最佳买卖股票时机含冷冻期
 */

// @lc code=start
class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0){
            return 0;
        }
        int n = prices.length;
        int dp0 = -prices[0];
        int dp1 = 0;
        int dp2 = 0;
        for(int i=1; i<n; i++){
            int newdp0 = Math.max(dp0, dp2-prices[i]);
            int newdp1 = dp0 + prices[i];
            int newdp2 = Math.max(dp1, dp2);
            dp0 = newdp0;
            dp1 = newdp1;
            dp2 = newdp2;
        }
        return Math.max(dp1, dp2);
    }
}

复杂度分析：

时间复杂度：$O(n)$。
空间复杂度：$O(1)$。