0%

leetcode-第196场周赛

Posted on Edited on In ,

第196场周赛

##1.判断能否形成等差数列

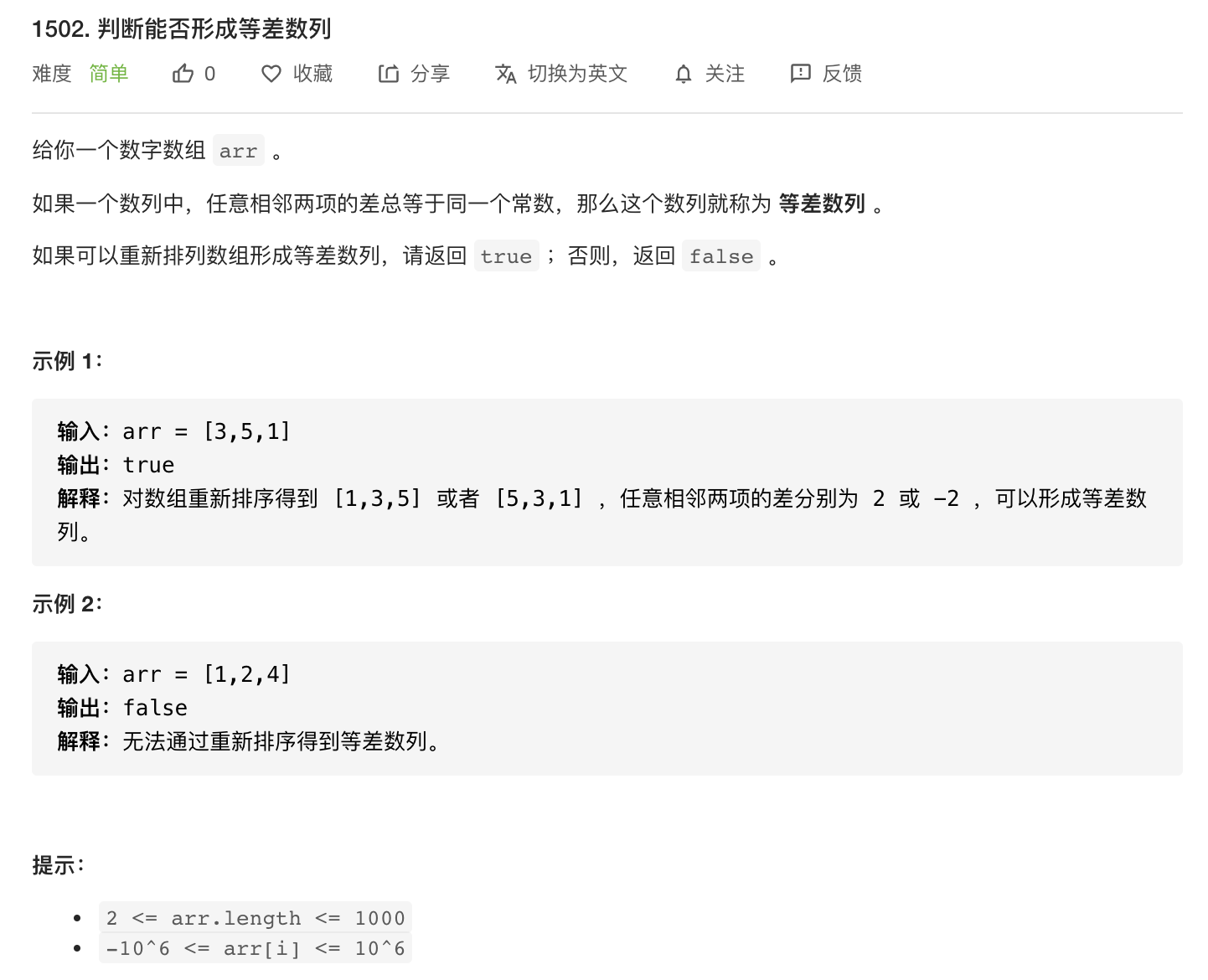
image1

先将数组排序，再利用等差数列的性质遍历一遍。

1
class Solution {
2
    public boolean canMakeArithmeticProgression(int[] arr) {
3
        if(arr==null || arr.length==0){
4
            return false;
5
        }
6
        if(arr.length==1){
7
            return true;
8
        }
9
        Arrays.sort(arr);
10
        int n = arr.length;
11
        int cha = arr[1]-arr[0];
12
        for(int i=2; i<n; i++){
13
            if(arr[i]-arr[i-1]!=cha){
14
                return false;
15
            }
16
        }
17
        return true;
18
    }
19
}

复杂度分析：

  • 时间复杂度：$O(nlogn+n)$。
  • 空间复杂度：$O(1)$。

2.所有蚂蚁掉下来前的最后一刻

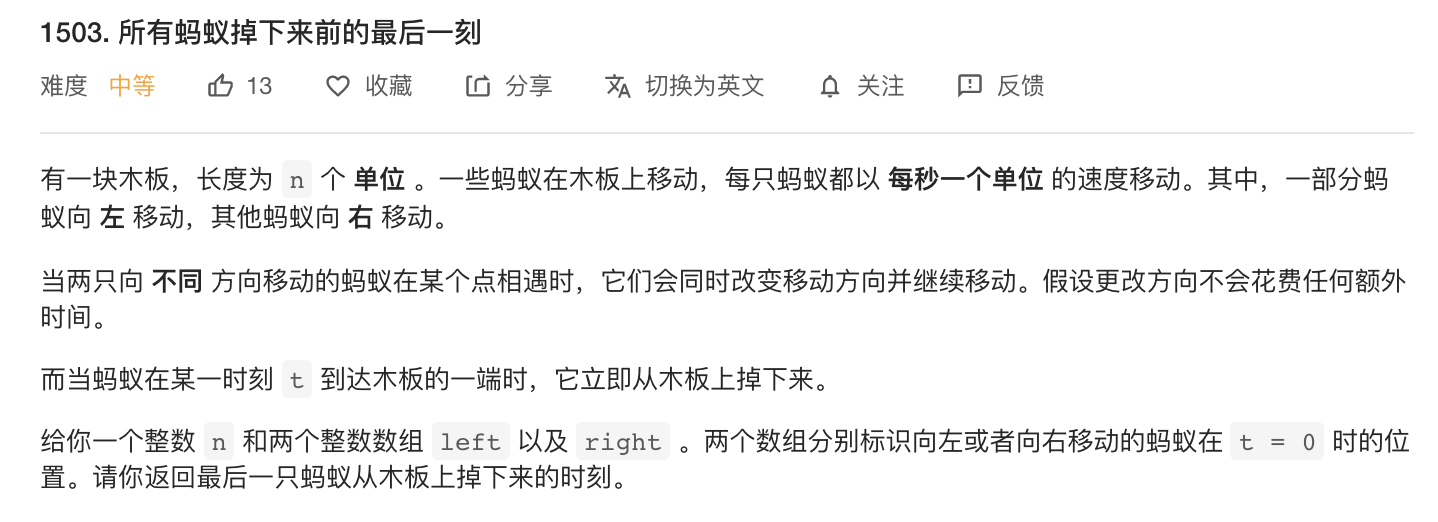
image2

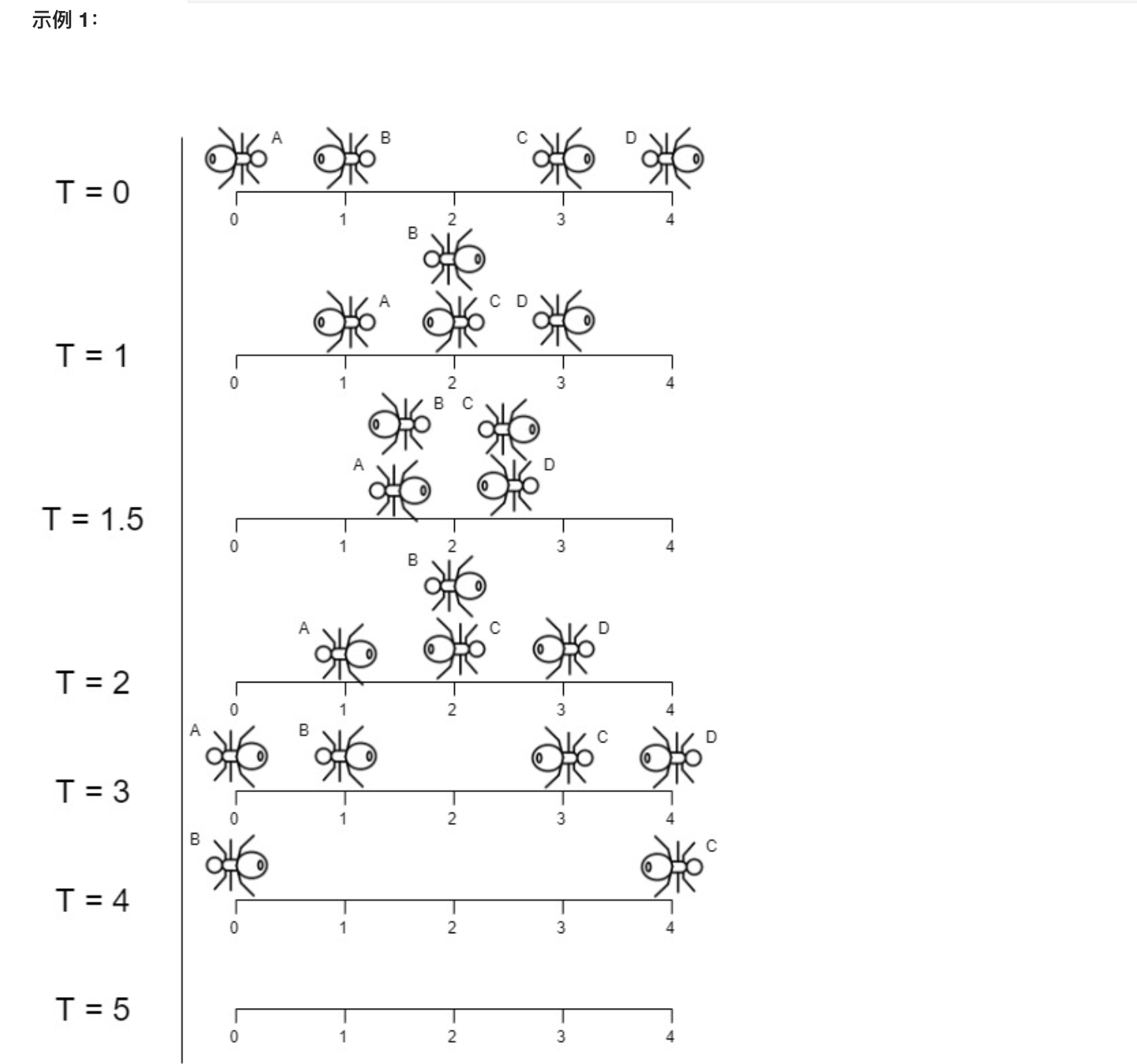
image3

image4

image5

两个蚂蚁相撞之后会互相调头，其实只要想成如果每只蚂蚁都长得一模一样，那么蚂蚁碰撞的调头就等于穿透了。知道了这一点，那么就可以直接让蚂蚁直接穿透爬行就好了，那么题目就变成了求单只最晚落地的蚂蚁，与碰撞无关。left数组中的蚂蚁求出到左边最晚时间，right数组中的蚂蚁求出到右边最晚时间，之后两者取较大值即可。

1
class Solution {
2
    public int getLastMoment(int n, int[] left, int[] right) {
3
        int ans = -1;
4
        for(int i=0; i<left.length; i++){
5
            ans = Math.max(ans, left[i]);
6
        }
7
        for(int i=0; i<right.length; i++){
8
            ans = Math.max(ans, n-right[i]);
9
        }
10
        return ans;
11
    }
12
}

时间复杂度：

  • 时间复杂度：$O(n)$，$n$为数组$left$和$right$的长度。
  • 空间复杂度：$O(1)$。

3.统计全1子矩形

image6

image7

首先动态规划，计算每个点前面连续的1的个数(行，包括自己)，即dp[i][j]=dp[i][j-1]+1，点为0的点不用计算，直接为0即可。然后开始循环遍历，每次计算以mat[i][j]为右下角的矩阵个数，并累加到sum中。

举例子，如下图的矩阵，我们现在计算以mat[2][2]为右下角所构成的矩阵：

1
[0,0,1]
2
[0,1,1]
3
[1,1,1]

首先是第三行dp[2][2]=3，所以最小长度为3，sum+=3。这里计算的矩阵只有第三行元素构成的矩阵：

1
[1,1,1],  [1,1],  [1]

向上遍历，第二行时，dp[1][2]=2，此时最小长度为2，sum+=2，这里计算的矩阵是第二、三行元素构成的矩阵：

1
[1]  [1,1]
2
[1], [1,1]

继续向上遍历，第一行时，dp[0][2]=1，此时最小长度为1，sum+=1，这里计算的矩阵是第一、二、三行元素构成的矩阵：

1
[1]
2
[1]
3
[1]

该点遍历结束。矩阵循环遍历结束后返回sum即可。因为这里计数的时候固定了子矩阵的右下角元素，所以不会重复计数。

1
class Solution {
2
    public int numSubmat(int[][] mat) {
3
        int m = mat.length;
4
        int n = mat[0].length;
5
        int[][] dp = new int[m][n];
6
        int sum = 0;
7
        for(int i=0; i<m; i++){
8
            dp[i][0] = mat[i][0];
9
        }
10
        for(int i=0; i<m; i++){
11
            for(int j=0; j<n; j++){
12
                if(mat[i][j] == 0){
13
                    dp[i][j] = 0;
14
                    continue;
15
                }
16
                if(j!=0){
17
                    dp[i][j] = dp[i][j-1] + 1;
18
                }
19
                int minlen = n+1;
20
                for(int k=i; k>=0; k--){
21
                    minlen = Math.min(minlen, dp[k][j]);
22
                    sum += minlen;
23
                }
24
            }
25
        }
26
        return sum;
27
    }
28
}

复杂度分析：

  • 时间复杂度：$O(mmn)$。
  • 空间复杂度：$O(m*n)$。

最多K次交换相邻数位后得到的最小整数

image8

image9

可以使用贪心策略，即每次交换都先将更小的数如0、1等换到较前面的位置去。这个过程中我们需要做两件事：

  • 找到较小数的位置
  • 计算交换需要用到的次数

找到较小数的位置我们可以使用哈希表来优化这一搜索的过程，即遍历一遍字符串，记录每个数出现的位置，之后在进行搜索的时候只需要查找哈希表就可得到位置。计算交换需要用到的次数不可以直接两个索引相减得到，因为我们实际上并没有交换原字符串中两个数的位置。需要使用树状数组来计算，首先初始化树状数组，在单点更新的时候都加1，即初始化交换次数，在每次交换的时候，就可以利用树状数组查询交换次数，并进行单点更新，此时单点更新需要减1，因为在$i$和$j(i<j)$进行交换的时候，$[i,j-1]$之间的数都往右移了一位，那么这些数之后需要交换的次数就可以因为这次交换而减1，例如2,3,4,1，再进行过一次交换后变为1,2,3,4，此时就不需要再次交换了，因为2,3,4在之前的一次交换中已经向右移动了一位，也相当于进行了交换。

1
class Solution {
2
    public String minInteger(String num, int k) {
3
        char[] s = num.toCharArray();
4
        int n = s.length;
5
6
        IntergerBIT bit = new IntergerBIT(s.length);
7
        for(int i=1; i<=n; i++){
8
            bit.update(i, 1);
9
        }
10
        Deque<Integer>[] dq = new Deque[10];
11
        for(int i=0; i<10; i++){
12
            dq[i] = new ArrayDeque(n);
13
        }
14
        for(int i=0; i<n; i++){
15
            dq[s[i]-'0'].add(i);
16
        }
17
        StringBuilder ans = new StringBuilder(n);
18
        for(int i=0; i<n; i++){
19
            for(int j=0; j<10; j++){
20
                if(!dq[j].isEmpty() && bit.query(dq[j].getFirst())<=k){
21
                    k -= bit.query(dq[j].getFirst());
22
                    bit.update(dq[j].getFirst()+1, -1);
23
                    dq[j].removeFirst();
24
                    ans.append((char)(j+'0'));
25
                    break;
26
                }
27
            }
28
        }
29
        return ans.toString();
30
    }
31
}
32
33
public class IntergerBIT {
34
    int[] data;
35
    int n;
36
37
    /**
38
     * 创建大小A[1...n]
39
     */
40
    public IntergerBIT(int n){
41
        this.n = n;
42
        this.data = new int[n+1];
43
    }
44
    /**
45
     * 查询A[1]+A[2]+...+A[i]
46
     */
47
    public int query(int i) {
48
        int sum = 0;
49
        while(i > 0){
50
            sum += data[i];
51
            i -= lowbit(i);
52
        }
53
        return sum;
54
    }
55
56
    public int query(int l, int r) {
57
        return query(r) - query(l - 1);
58
    }
59
60
    /**
61
     * 将A[i]更新为A[i]+mod
62
     */
63
    public void update(int i, int mod) {
64
        if(i <= 0){
65
            return;
66
        }
67
        while(i<=n){
68
            data[i] += mod;
69
            i += lowbit(i);
70
        }
71
    }
72
73
    /**
74
     * 将A全部清0
75
     */
76
    public void clear() {
77
        Arrays.fill(data, 0);
78
    }
79
80
    @Override
81
    public String toString() {
82
        StringBuilder builder = new StringBuilder();
83
        for (int i = 1; i <= n; i++) {
84
            builder.append(query(i) - query(i - 1)).append(' ');
85
        }
86
        return builder.toString();
87
    }
88
89
    public static int lowbit(int x) {
90
        return x & (-x);
91
    }
92
}

复杂度分析：

  • 时间复杂度：$O(nlogn)$。
  • 空间复杂度：$O(n)$。