第197场周赛

1.好数对的数目

因为数据量不大，可以直接用暴力方法求解。

class Solution {
    public int numIdenticalPairs(int[] nums) {
        int n = nums.length;
        int count = 0;
        for(int i=0; i<n; i++){
            for(int j=i+1; j<n; j++){
                if(nums[i] == nums[j]){
                    count++;
                }
            }
        }
        return count;
    }
}

复杂度分析：

时间复杂度：$O(n^2)$。
空间复杂度：$O(1)$。

也可以用空间换时间，将时间复杂度降到$O(n)$。举个例子，如果1出现了两次，那么好数对的个数为1，如果1出现了三次，那么好数对的个数为2+1，出现了四次，那么好数对的个数为3+2+1。可以发现这是一个等差数列，那么我们可以先计数数字的个数，再用等差数列求和公式计算好数对个数。

class Solution {
    public int numIdenticalPairs(int[] nums) {
        int[] cnt = new int[101];
        for(int x : nums){
            cnt[x]++;
        }
        int ans = 0;
        for(int i = 0; i <= 100; i++){
            ans += cnt[i] * (cnt[i] - 1) / 2;
        }
        return ans;
    }
}

2.仅含1的子串数

思路类似于子矩阵，当子串为1的时候，仅含1的子串数为1。当子串为11的时候，仅含1的子串数为1+2。当子串数为111的时候，仅含1的子串数为1+2+3，以此类推。我们可以使用双指针来找寻仅含1的子串，左指针指向子串最左端，右指针向右移动，如果右指针当前指向1，结果就累加right-left，否则将左指针指向右指针，直到右指针到达边界。

class Solution {
    public int numSub(String s) {
        int len = s.length();
        int mode = (int) 1e9 + 7;
        int left = -1;
        int right = 0;
        int count = 0;
        while(right<len){
            if(s.charAt(right) == '0'){
                left = right;
                right++;
            }else{
                count += (right-left)%mode;
                count %= mode;
                right++;
            }
        }
        return count;
    }
}

复杂度分析：

时间复杂度：$O(n)$。
空间复杂度：$O(1)$。

3.概率最大的路径

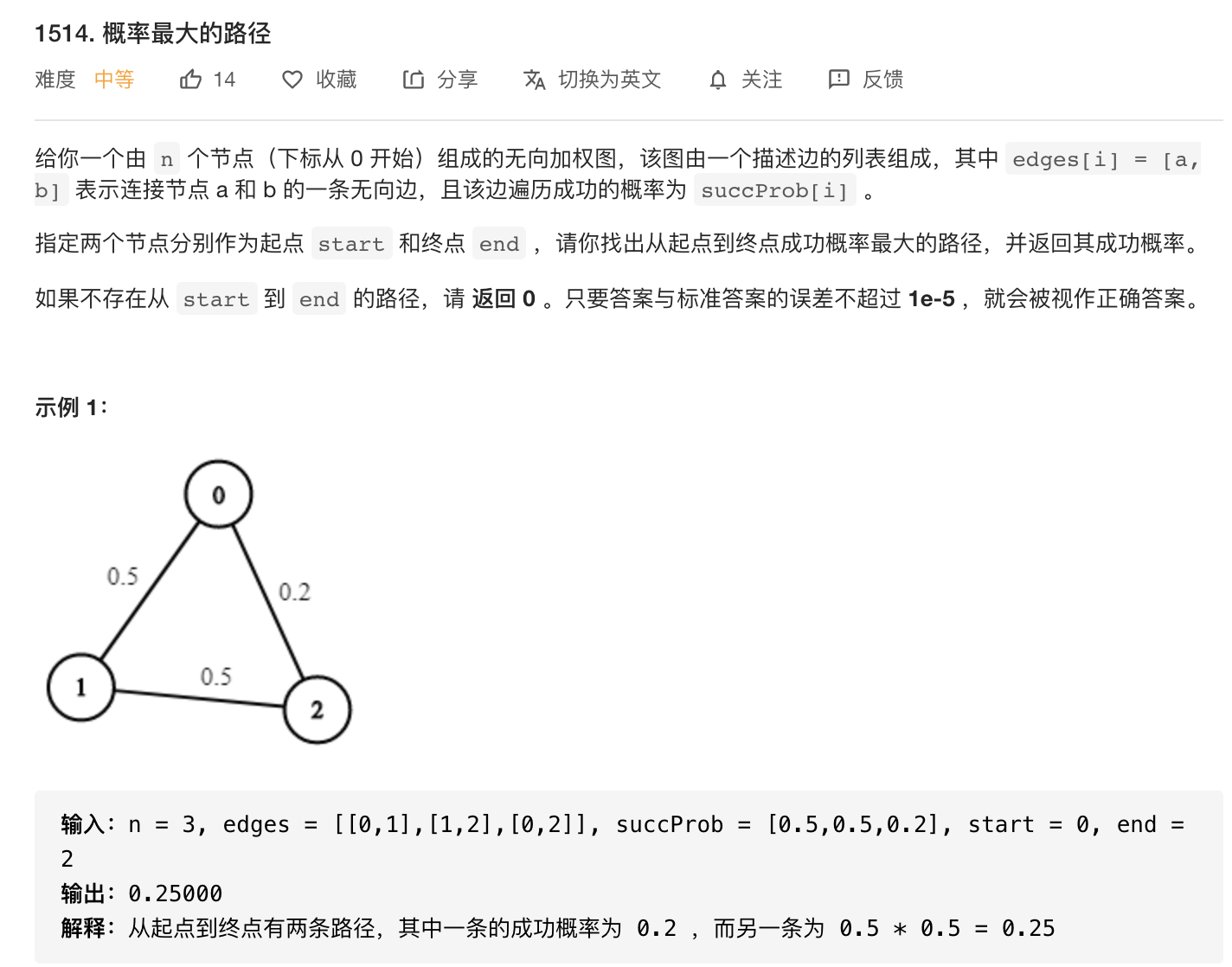
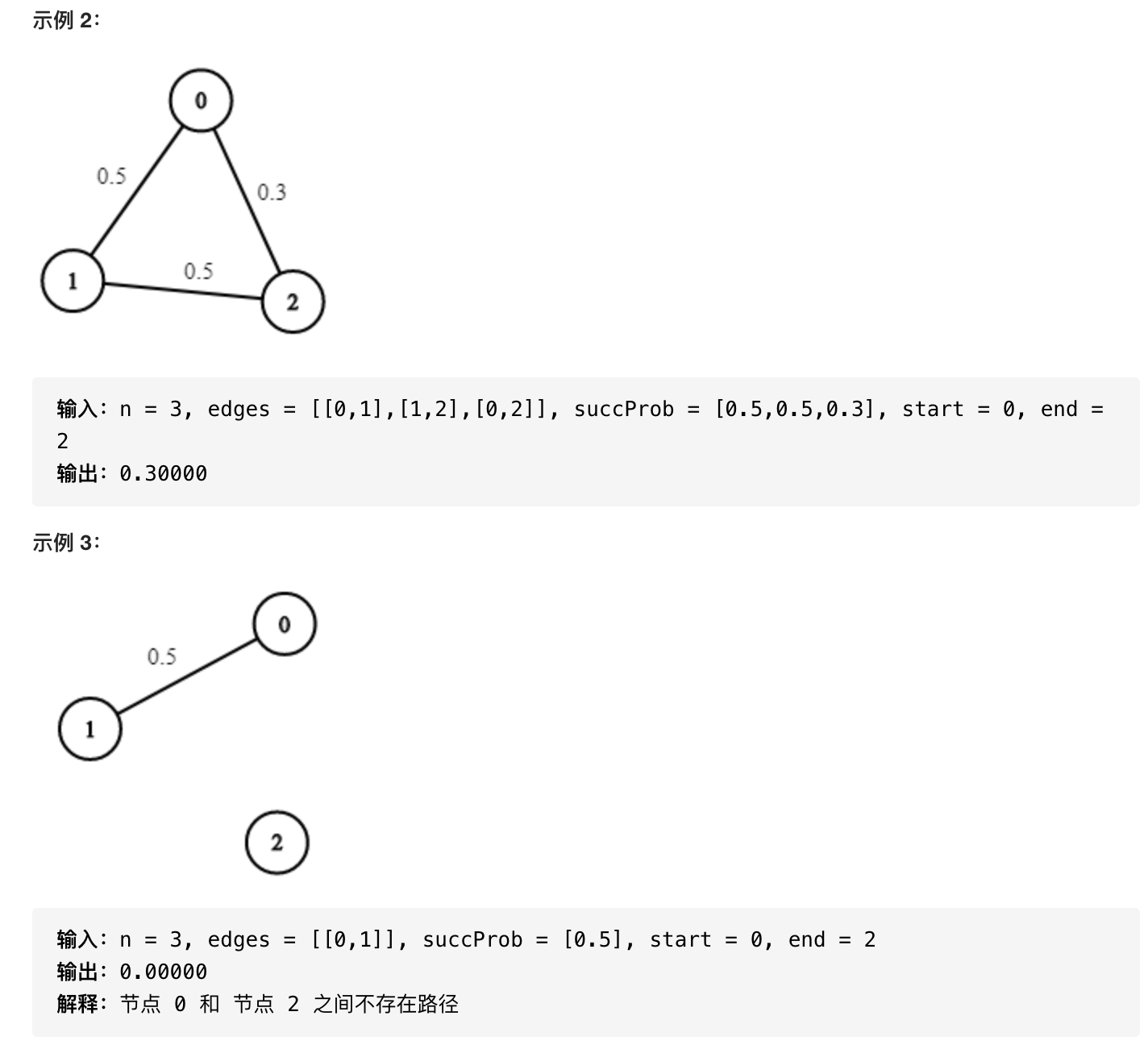
采用贪心策略，每次选取剩余概率最大的一条边。由于所有边的权重都是处于0到1之间，所以如果存在一个不在集合中的d使得s -> ... -> d -> ... -> c比当前s -> ... -> c更大，那么s到d的路径的概率必然大于s到c的概率，那么d必然会比c之前被选中，加入集合。这于d不在集合中相矛盾。这就变成了最短路问题。

或者换一个角度想，对概率相乘取对数，那么乘法就变成了对数加法，如果概率相乘越大，那么对数加法就越小，就可以等价于找一个最短路。最短路算法我们可以使用dijkstra算法。

这里使用了堆优化过的dijkstra算法，还有需要一点改变：dijkstra算法中初始点的权重设为0，我们这里需要设为1，转换为对数就是0。在dijkstra算法中初始每条路径权重都为无穷大，我们这里需要初始化为0，转换为对数就是无穷大。

class Solution {
    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
        Node[] nodes = new Node[n];
        for(int i=0; i<n; i++){
            nodes[i] = new Node();
            nodes[i].id = i;
          	//权重初始化为0
            nodes[i].p = 0;
        }
        for(int i=0; i<edges.length; i++){
            Node a = nodes[edges[i][0]];
            Node b = nodes[edges[i][1]];
            Edge e = new Edge();
            e.a = a;
            e.b = b;
            e.p = succProb[i];
            a.adj.add(e);
            b.adj.add(e);
        }
				//大根堆，每次取出最大值
        TreeSet<Node> set = new TreeSet<>((a,b) -> a.p==b.p ? Integer.compare(a.id, b.id) : Double.compare(b.p, a.p));
      	//起始点权重初始化为1
        nodes[start].p = 1;
        set.add(nodes[start]);
        while(!set.isEmpty()){
            Node head = set.pollFirst();
            for(Edge e : head.adj){
                Node node = e.other(head);
                double p = e.p * head.p;
              	//概率比当前点概率大，更新
                if(p > node.p){
                    set.remove(node);
                    node.p = p;
                    set.add(node);
                }
            }
        }
        return nodes[end].p;
    }
}

class Edge{
    Node a;
    Node b;
    double p;

    public Node other(Node x){
        return a == x ? b : a;
    }
}

class Node{
    double p;
    List<Edge> adj = new ArrayList();
    int id;
}

复杂度分析：

时间复杂度：$O(|E|+|V|log|V|)$。
空间复杂度：$O(|V|)$。

4.服务中心的最佳位置

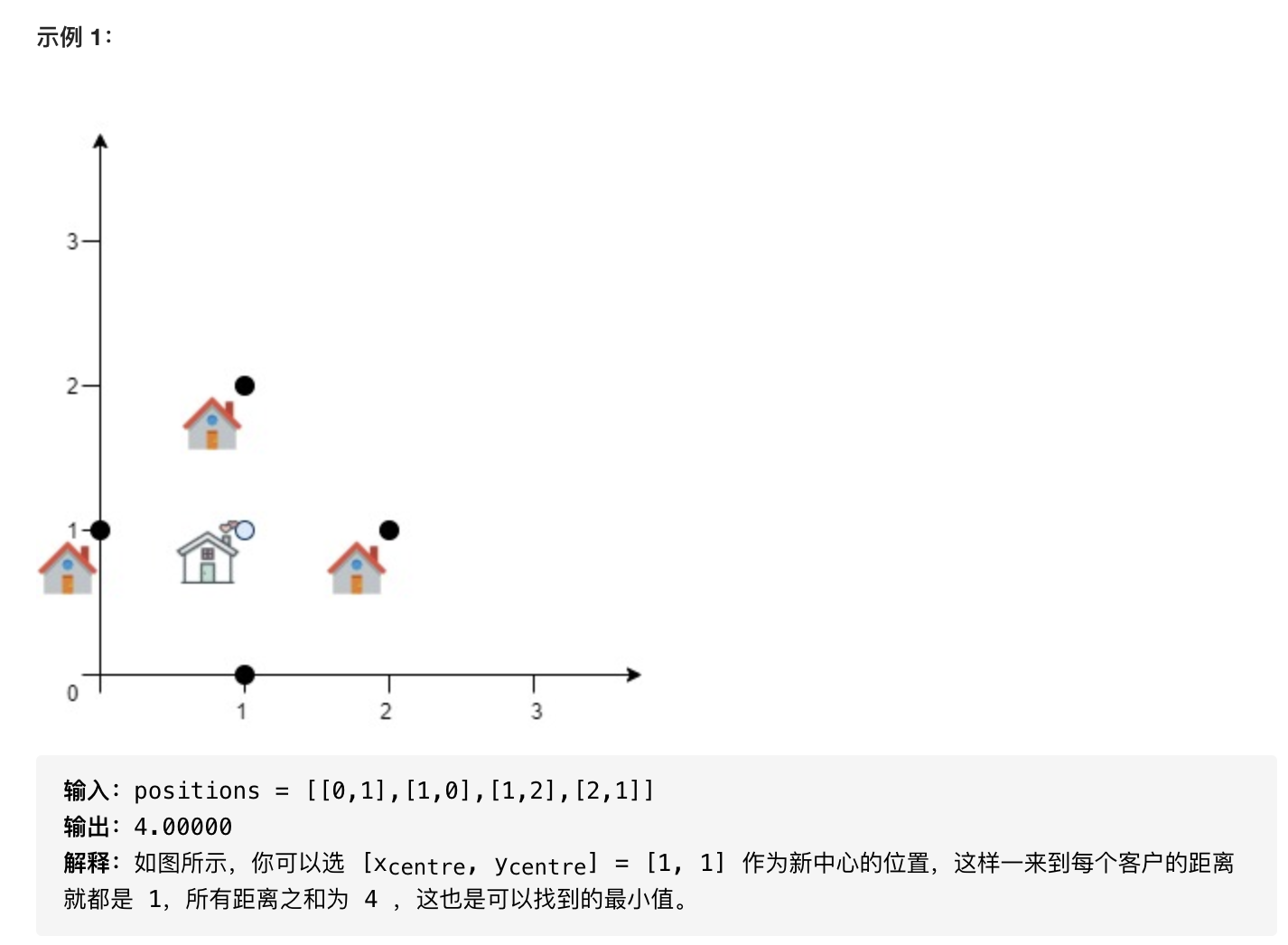
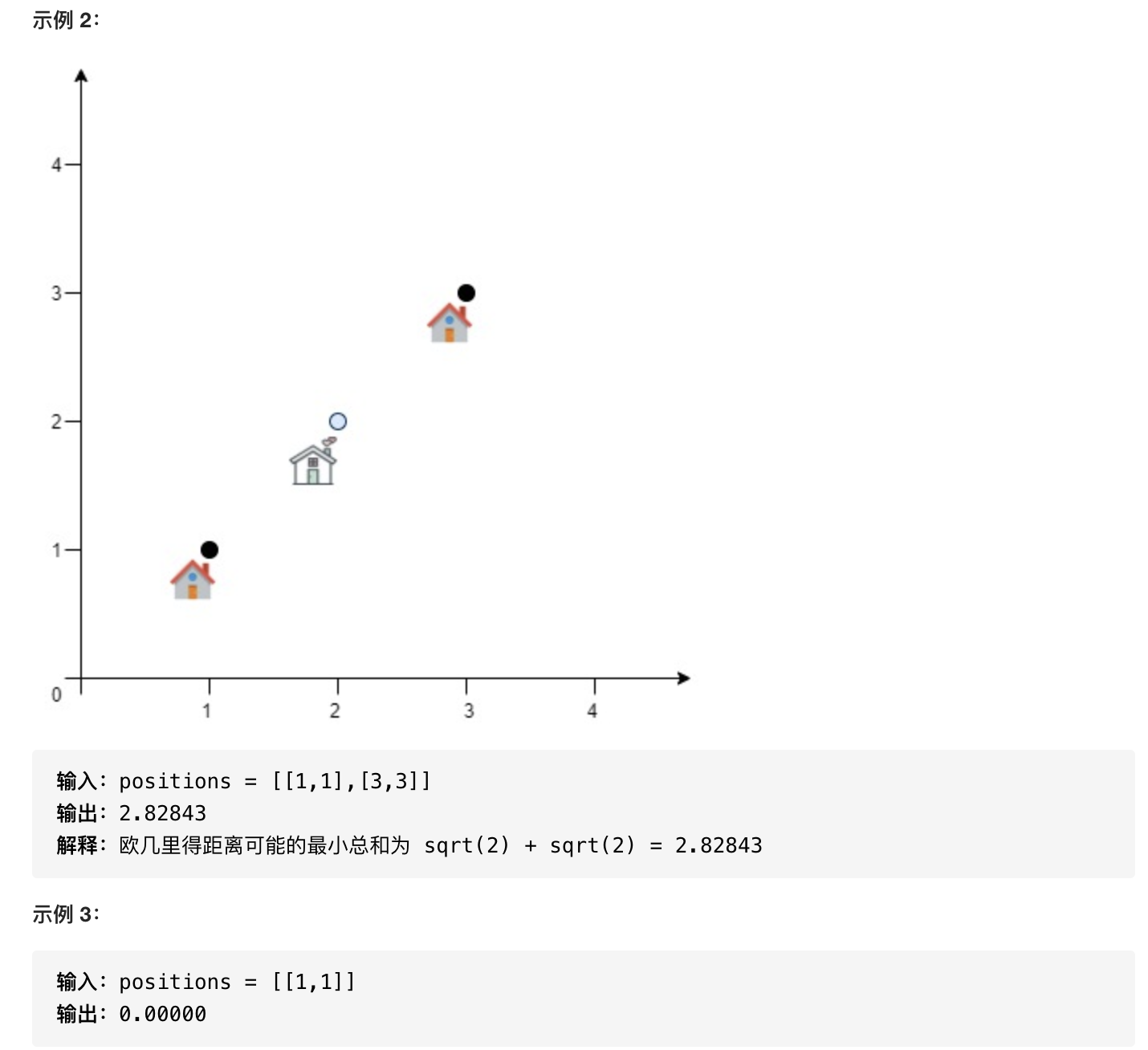
目标函数是一个凸函数，可以用很多方法，例如三分法，梯度下降法，模拟退火等等。

public class Solution {

    public double getMinDistSum(int[][] positions) {
        Random random = new Random();
        double[] dist = new double[positions.length];
        SimulatedAnnealing<double[]> sa = new SimulatedAnnealing<double[]>(1e-10, 1e-5, 0.98, random) {
            @Override
            public double[] next(double[] old, double temperature) {
                double dx = (random.nextDouble() - 0.5) * temperature;
                double dy = (random.nextDouble() - 0.5) * temperature;
                double[] ans = new double[2];
                ans[0] = old[0] + dx;
                ans[1] = old[1] + dy;
                for (int i = 0; i < 2; i++) {
                    ans[i] = Math.max(0, ans[i]);
                    ans[i] = Math.min(100, ans[i]);
                }
                return ans;
            }

            @Override
            public double eval(double[] status) {
                for(int i = 0; i < positions.length; i++){
                    double dx = status[0] - positions[i][0];
                    double dy = status[1] - positions[i][1];
                    double d = Math.sqrt(dx * dx + dy * dy);
                    dist[i] = d;
                }
                return -Arrays.stream(dist).sum();
            }
        };

        for(int i = 0; i < 20; i++){
            sa.optimize(200, new double[]{random.nextDouble() * 100, random.nextDouble() * 100});
        }
        double ans = -sa.weightOfBest();
        return ans;
    }
}

abstract class SimulatedAnnealing<S> {
    public SimulatedAnnealing(double threshold, double k, double reduce) {
        this(threshold, k, reduce, new Random());
    }

    public SimulatedAnnealing(double threshold, double k, double reduce, Random random) {
        this.threshold = threshold;
        this.k = k;
        this.reduce = reduce;
        this.random = random;
    }

    public abstract S next(S old, double temperature);

    public abstract double eval(S status);

    public void abandon(S old) {
    }

    public void optimize(double temperature, S init) {
        S now = init;
        double weight = eval(now);
        double t = temperature;
        while (t > threshold) {
            S next = next(now, t);
            double nextWeight = eval(next);
            if (nextWeight > weight || random.nextDouble() < Math.exp((nextWeight - weight) / (k * t))) {
                abandon(now);
                now = next;
                weight = nextWeight;
            }
            t *= reduce;
        }

        if (best == null || bestWeight < weight) {
            best = now;
            bestWeight = weight;
        }
    }

    public S getBest() {
        return best;
    }

    public double weightOfBest() {
        return bestWeight;
    }

    private S best;
    private double bestWeight = -1e100;
    private Random random;
    private double threshold;
    /**
     * The larger k is, the more possible to challenge
     */
    private double k;
    /**
     * The smaller reduce is, the faster to reduce temperature
     */
    private double reduce;
}

剩下的事就是调参了。

1	public class Solution {
2
3	public double getMinDistSum(int[][] positions) {
4	Random random = new Random();
5	double[] dist = new double[positions.length];
6	SimulatedAnnealing<double[]> sa = new SimulatedAnnealing<double[]>(1e-10, 1e-5, 0.98, random) {
7	@Override
8	public double[] next(double[] old, double temperature) {
9	double dx = (random.nextDouble() - 0.5) * temperature;
10	double dy = (random.nextDouble() - 0.5) * temperature;
11	double[] ans = new double[2];
12	ans[0] = old[0] + dx;
13	ans[1] = old[1] + dy;
14	for (int i = 0; i < 2; i++) {
15	ans[i] = Math.max(0, ans[i]);
16	ans[i] = Math.min(100, ans[i]);
17	}
18	return ans;
19	}
20
21	@Override
22	public double eval(double[] status) {
23	for(int i = 0; i < positions.length; i++){
24	double dx = status[0] - positions[i][0];
25	double dy = status[1] - positions[i][1];
26	double d = Math.sqrt(dx * dx + dy * dy);
27	dist[i] = d;
28	}
29	return -Arrays.stream(dist).sum();
30	}
31	};
32
33	for(int i = 0; i < 20; i++){
34	sa.optimize(200, new double[]{random.nextDouble() * 100, random.nextDouble() * 100});
35	}
36	double ans = -sa.weightOfBest();
37	return ans;
38	}
39	}
40
41	abstract class SimulatedAnnealing<S> {
42	public SimulatedAnnealing(double threshold, double k, double reduce) {
43	this(threshold, k, reduce, new Random());
44	}
45
46	public SimulatedAnnealing(double threshold, double k, double reduce, Random random) {
47	this.threshold = threshold;
48	this.k = k;
49	this.reduce = reduce;
50	this.random = random;
51	}
52
53	public abstract S next(S old, double temperature);
54
55	public abstract double eval(S status);
56
57	public void abandon(S old) {
58	}
59
60	public void optimize(double temperature, S init) {
61	S now = init;
62	double weight = eval(now);
63	double t = temperature;
64	while (t > threshold) {
65	S next = next(now, t);
66	double nextWeight = eval(next);
67	if (nextWeight > weight \|\| random.nextDouble() < Math.exp((nextWeight - weight) / (k * t))) {
68	abandon(now);
69	now = next;
70	weight = nextWeight;
71	}
72	t *= reduce;
73	}
74
75	if (best == null \|\| bestWeight < weight) {
76	best = now;
77	bestWeight = weight;
78	}
79	}
80
81	public S getBest() {
82	return best;
83	}
84
85	public double weightOfBest() {
86	return bestWeight;
87	}
88
89	private S best;
90	private double bestWeight = -1e100;
91	private Random random;
92	private double threshold;
93	/**
94	* The larger k is, the more possible to challenge
95	*/
96	private double k;
97	/**
98	* The smaller reduce is, the faster to reduce temperature
99	*/
100	private double reduce;
101	}

1	class Solution {
2	public int numIdenticalPairs(int[] nums) {
3	int n = nums.length;
4	int count = 0;
5	for(int i=0; i<n; i++){
6	for(int j=i+1; j<n; j++){
7	if(nums[i] == nums[j]){
8	count++;
9	}
10	}
11	}
12	return count;
13	}
14	}

1	class Solution {
2	public int numIdenticalPairs(int[] nums) {
3	int[] cnt = new int[101];
4	for(int x : nums){
5	cnt[x]++;
6	}
7	int ans = 0;
8	for(int i = 0; i <= 100; i++){
9	ans += cnt[i] * (cnt[i] - 1) / 2;
10	}
11	return ans;
12	}
13	}

1	class Solution {
2	public int numSub(String s) {
3	int len = s.length();
4	int mode = (int) 1e9 + 7;
5	int left = -1;
6	int right = 0;
7	int count = 0;
8	while(right<len){
9	if(s.charAt(right) == '0'){
10	left = right;
11	right++;
12	}else{
13	count += (right-left)%mode;
14	count %= mode;
15	right++;
16	}
17	}
18	return count;
19	}
20	}

1	class Solution {
2	public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
3	Node[] nodes = new Node[n];
4	for(int i=0; i<n; i++){
5	nodes[i] = new Node();
6	nodes[i].id = i;
7	//权重初始化为0
8	nodes[i].p = 0;
9	}
10	for(int i=0; i<edges.length; i++){
11	Node a = nodes[edges[i][0]];
12	Node b = nodes[edges[i][1]];
13	Edge e = new Edge();
14	e.a = a;
15	e.b = b;
16	e.p = succProb[i];
17	a.adj.add(e);
18	b.adj.add(e);
19	}
20	//大根堆，每次取出最大值
21	TreeSet<Node> set = new TreeSet<>((a,b) -> a.p==b.p ? Integer.compare(a.id, b.id) : Double.compare(b.p, a.p));
22	//起始点权重初始化为1
23	nodes[start].p = 1;
24	set.add(nodes[start]);
25	while(!set.isEmpty()){
26	Node head = set.pollFirst();
27	for(Edge e : head.adj){
28	Node node = e.other(head);
29	double p = e.p * head.p;
30	//概率比当前点概率大，更新
31	if(p > node.p){
32	set.remove(node);
33	node.p = p;
34	set.add(node);
35	}
36	}
37	}
38	return nodes[end].p;
39	}
40	}
41
42	class Edge{
43	Node a;
44	Node b;
45	double p;
46
47	public Node other(Node x){
48	return a == x ? b : a;
49	}
50	}
51
52	class Node{
53	double p;
54	List<Edge> adj = new ArrayList();
55	int id;
56	}