0%

leetcode每日一题-交错字符串

Posted on In ,

交错字符串

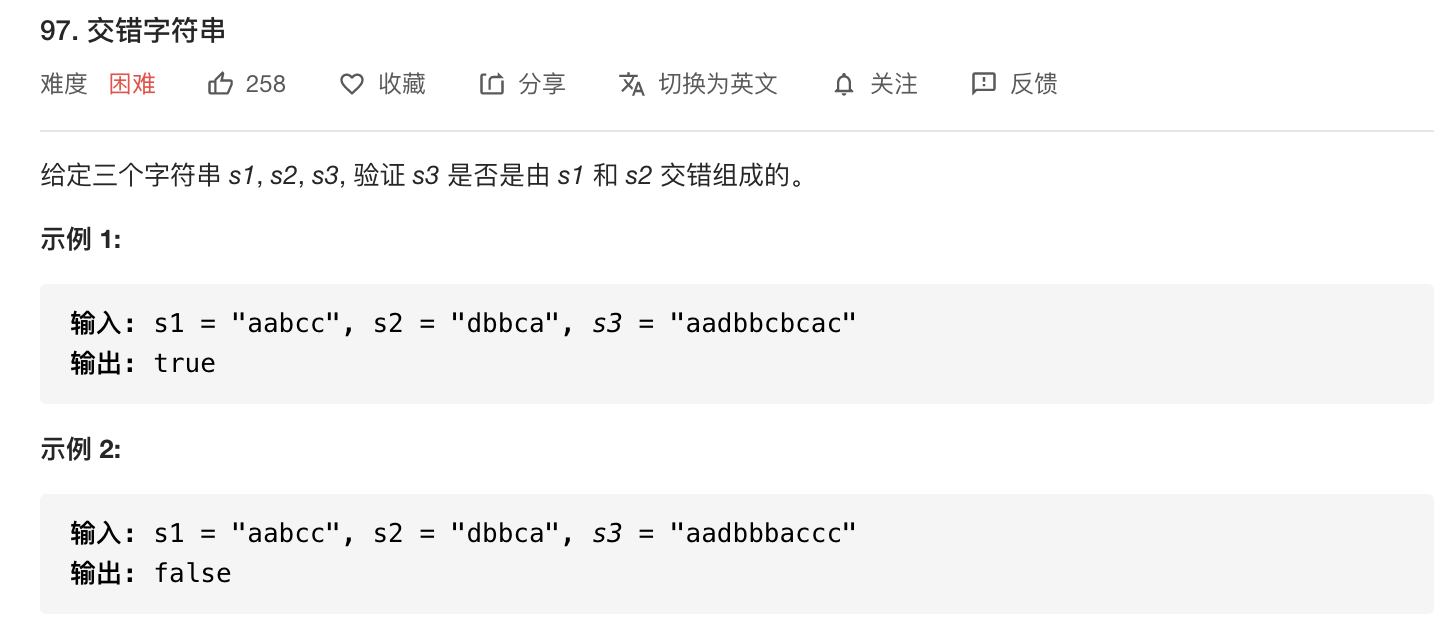
image1

首先判断$s1$的长度和$s2$的长度加起来是否等于$s3$，如果不等于，那么就肯定不对。之后看$s1$的前$i$个字符和$s2$的前$j$个字符是否可以组成$s3$的前$i+j$个字符，如果$s1$的第$i$个字符（对应数组中下标$i-1$）与$s3$的第$i+j$个字符（对应数组中下标$i+j-1$）相等，就要看$s1$的前$i-1$个字符和$s2$的前$j$个字符是否可以组成$s3$的前$i+j-1$个字符。如果$s2$的第$j$个字符与$s3$的第$i+j$个字符相等，也是同理，如此我们记$dp[i][j]$为$s1$的前$i$个字符和$s2$的前$j$个字符是否可以组成$s3$的前$i+j$个字符的状态，状态转移方程为：
$$
dp[i][j] = (dp[i-1][j] \wedge s1[i-1]==s3[i+j-1]) \vee (dp[i][j-1]\wedge s2[j-1]==s3[i+j-1])
$$
其中边界条件为$dp[0][0]=true$

1
class Solution {
2
    public boolean isInterleave(String s1, String s2, String s3) {
3
        int n = s1.length();
4
        int m = s2.length();
5
        int s = s3.length();
6
        if(n+m != s){
7
            return false;
8
        }
9
        boolean[][] dp = new boolean[n+1][m+1];
10
        dp[0][0] = true;
11
        for(int i=0; i<=n; i++){
12
            for(int j=0; j<=m; j++){
13
                int p = i+j-1;
14
                if(i>0){
15
                    dp[i][j] = dp[i][j] || (dp[i-1][j]&&s1.charAt(i-1)==s3.charAt(p));
16
                }
17
                if(j>0){
18
                    dp[i][j] = dp[i][j] || (dp[i][j-1]&&s2.charAt(j-1)==s3.charAt(p));
19
                }
20
            }
21
        }
22
        return dp[n][m];
23
    }
24
}

复杂度分析：

  • 时间复杂度：$O(mn)$。
  • 空间复杂度：$O(mn)$。

可以使用滚动数组的思想进一步优化空间复杂度到$O(m)$。

1
class Solution {
2
    public boolean isInterleave(String s1, String s2, String s3) {
3
        int n = s1.length();
4
        int m = s2.length();
5
        int s = s3.length();
6
        if(n+m != s){
7
            return false;
8
        }
9
        boolean[] dp = new boolean[m+1];
10
        dp[0] = true;
11
        for(int i=0; i<=n; i++){
12
            for(int j=0; j<=m; j++){
13
                int p = i+j-1;
14
                if(i > 0){
15
                    dp[j] = dp[j] && s1.charAt(i-1)==s3.charAt(p);
16
                }
17
                if(j > 0){
18
                    dp[j] = dp[j] || (dp[j-1] && s2.charAt(j-1)==s3.charAt(p));
19
                }
20
            }
21
        }
22
        return dp[m];
23
    }
24
}

也可以使用DFS回溯+记忆化数组来解决：

1
class Solution {
2
    private Boolean[][] memo;
3
    public boolean isInterleave(String s1, String s2, String s3) {
4
        int n = s1.length();
5
        int m = s2.length();
6
        int s = s3.length();
7
        if(n+m != s){
8
            return false;
9
        }
10
        memo = new Boolean[n+1][m+1];
11
        return check(0,0,0,s1,s2,s3);
12
    }
13
14
    public boolean check(int i, int j, int k, String s1, String s2, String s3){
15
        if(k >= s3.length()){
16
            return true;
17
        }
18
        if(memo[i][j] != null){
19
            return memo[i][j];
20
        }
21
        boolean valid = false;
22
        if(i<s1.length() && s1.charAt(i)==s3.charAt(k)){
23
            valid = valid || check(i+1, j, k+1, s1, s2, s3);
24
        }
25
        if(j<s2.length() && s2.charAt(j)==s3.charAt(k)){
26
            valid = valid || check(i, j+1, k+1, s1, s2, s3);
27
        }
28
        memo[i][j] = valid;
29
        return valid;
30
    }
31
}