最小路径和
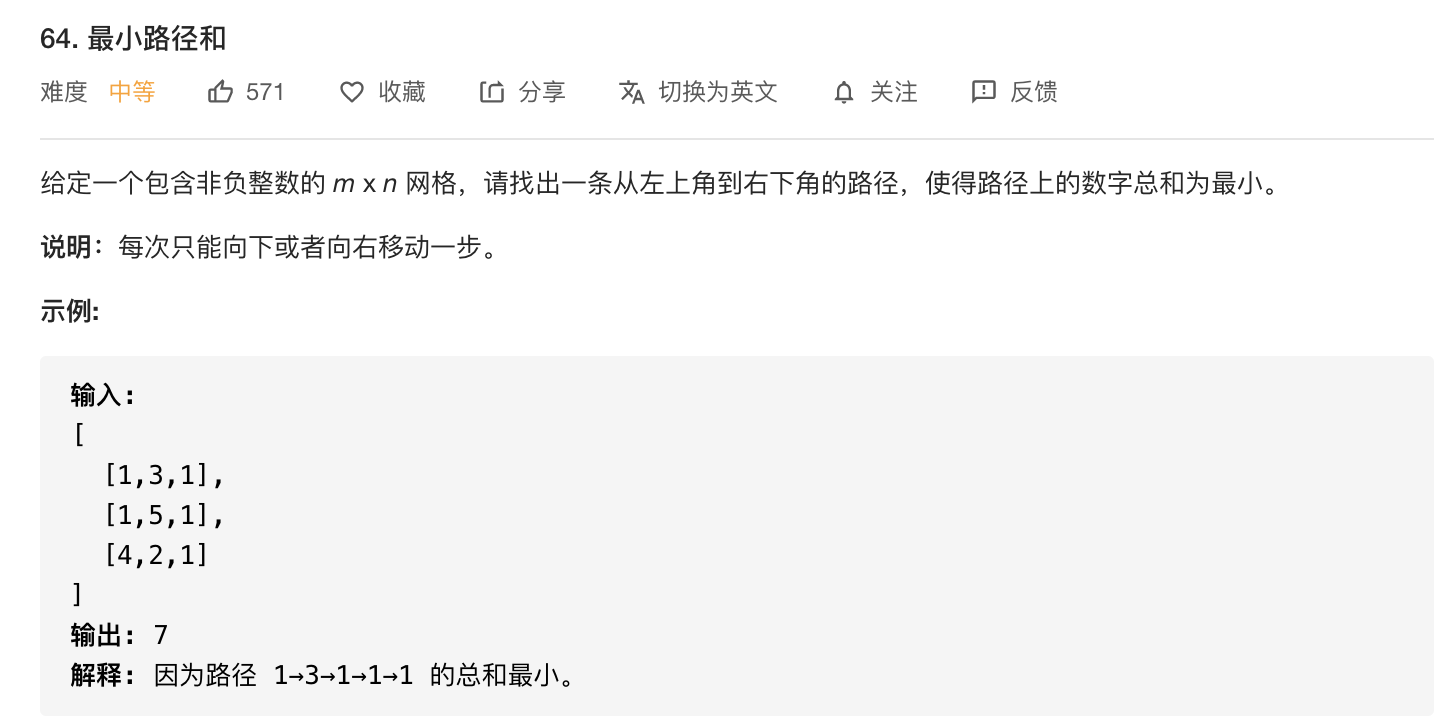
典型的动态规划题,记$dp[i][j]$为$(i,j)$处的最小路径和,因为只能向下或者向右走,状态转移方程为:
$$
dp[i][j] = min(dp[i-1][j],dp[i][j-1])+grid[i][j]
$$
最后结果就是终点处的值$dp[m-1][n-1]$。
1 | class Solution { |
2 | public int minPathSum(int[][] grid) { |
3 | int m = grid.length; |
4 | int n = grid[0].length; |
5 | int[][] dp = new int[m][n]; |
6 | dp[0][0] = grid[0][0]; |
7 | for(int i=1; i<m; i++){ |
8 | dp[i][0] = dp[i-1][0] + grid[i][0]; |
9 | } |
10 | for(int j=1; j<n; j++){ |
11 | dp[0][j] = dp[0][j-1] + grid[0][j]; |
12 | } |
13 | for(int i=1; i<m; i++){ |
14 | for(int j=1; j<n; j++){ |
15 | dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j]; |
16 | } |
17 | } |
18 | return dp[m-1][n-1]; |
19 | } |
20 | } |
复杂度分析:
- 时间复杂度:$O(mn)$。
- 空间复杂度:$O(mn)$。
可以使用滚动数组优化空间复杂度至$O(n)$。
1 | class Solution { |
2 | public int minPathSum(int[][] grid) { |
3 | int m = grid.length; |
4 | int n = grid[0].length; |
5 | int[] dp = new int[n]; |
6 | dp[0] = grid[0][0]; |
7 | for(int i=1; i<n; i++){ |
8 | dp[i] = dp[i-1] + grid[0][i]; |
9 | } |
10 | for(int i=1; i<m; i++){ |
11 | for(int j=0; j<n; j++){ |
12 | if(j == 0){ |
13 | dp[0] = dp[0] + grid[i][0]; |
14 | continue; |
15 | } |
16 | dp[j] = Math.min(dp[j],dp[j-1])+grid[i][j]; |
17 | } |
18 | } |
19 | return dp[n-1]; |
20 | } |
21 | } |