分割数组的最大值
方法一:动态规划
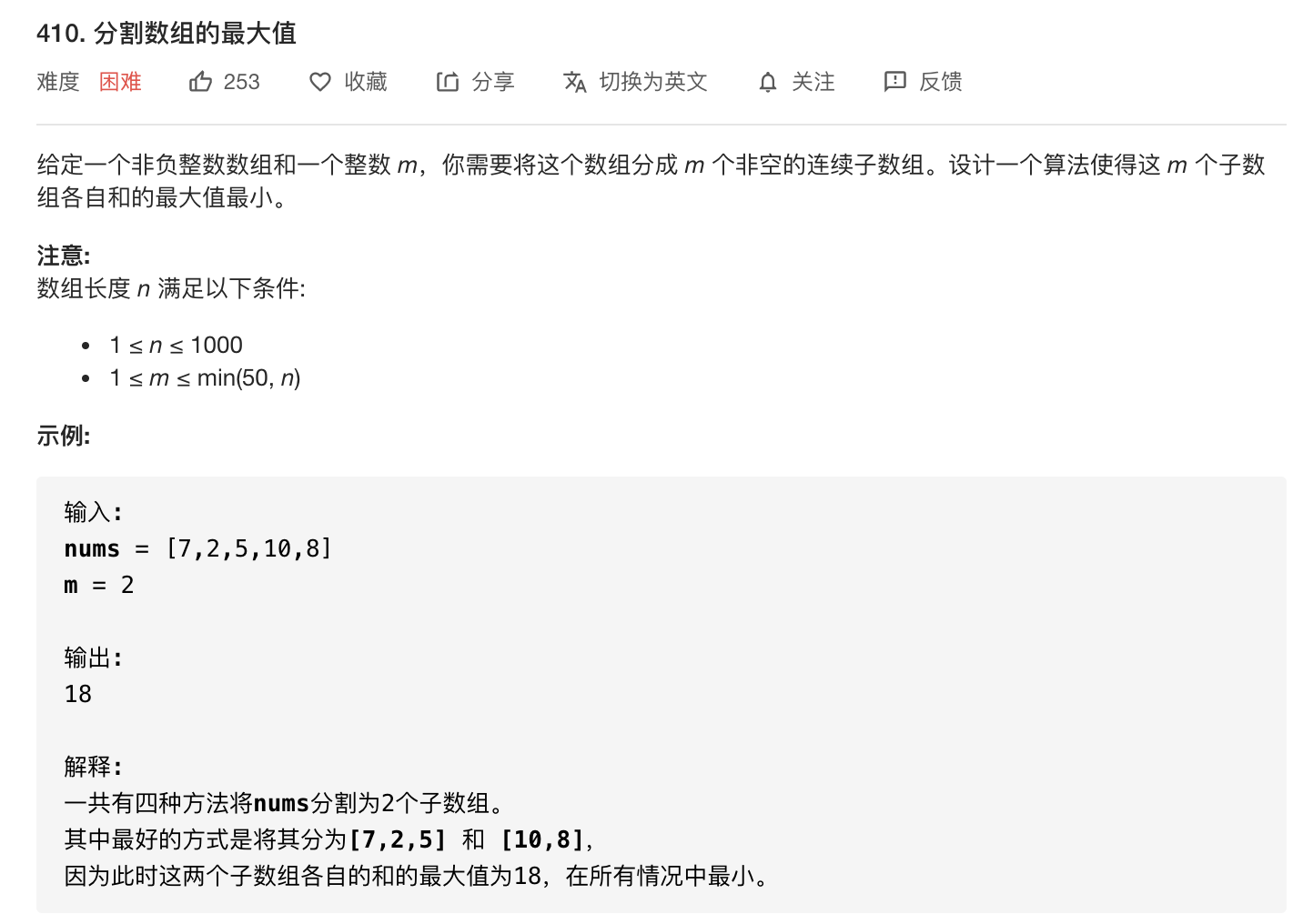
「将数组分割为 m** 段,求……」是动态规划题目常见的问法。
可以令dp[i][j]表示将数组的前i个数分割为j段所能得到的最大连续子数组之和的最小值。在进行状态转移时,我们可以考虑第j段的具体范围,即我们可以枚举k,其中前k个数被分割为j-1段,而第k+1个数到第i个数为第j段。此时,这j段子数组中的最大值,就等于dp[k][j-1]和sub(k+1,i)之间的较大值,其中sub(i,j)表示数组下标在$[i,j]$之间的数的和。
$$
dp[i][j] = min(max(dp[k][j-1],sub(k+1,i))),k \in [0,i-1]
$$
初始化的时候可以将数组中的值初始化为最大值,这样不合法的状态($i<j$)转移时就不会产生影响。同时需要将dp[0][0]初始化为0。
1 | class Solution { |
2 | public int splitArray(int[] nums, int m) { |
3 | int n = nums.length; |
4 | int[][] dp = new int[n+1][m+1]; |
5 | for(int i=0; i<=n; i++){ |
6 | Arrays.fill(dp[i], Integer.MAX_VALUE); |
7 | } |
8 | int[] sum = new int[n+1]; |
9 | for(int i=0; i<n; i++){ |
10 | sum[i+1] = sum[i] + nums[i]; |
11 | } |
12 | dp[0][0] = 0; |
13 | for(int i=1; i<=n; i++){ |
14 | for(int j=1; j<=Math.min(m,i); j++){ |
15 | for(int k=0; k<i; k++){ |
16 | dp[i][j] = Math.min(dp[i][j], Math.max(dp[k][j-1],sum[i]-sum[k])); |
17 | } |
18 | } |
19 | } |
20 | return dp[n][m]; |
21 | |
22 | } |
23 | } |
复杂度分析:
- 时间复杂度:$O(n^2m)$。$n$是数组的长度
- 空间复杂度:$O(nm)$。
方法二:二分查找
「使……最大值尽可能小」是二分搜索题目常见的问法。
分析可得结果的最小值应该为数组中的最大值,而最大值应该为数组中所有元素的和,即在$[max(nums),sum(nums)]$区间内,那么可以在这个区间范围内进行查找。具体做法就是:
贪心地模拟分割的过程,从前到后遍历数组,用 sum 表示当前分割子数组的和,cnt 表示已经分割出的子数组的数量(包括当前子数组),那么每当 sum 加上当前值超过了 x,我们就把当前取的值作为新的一段分割子数组的开头,并将 cnt 加 1。遍历结束后验证是否 cnt 不超过 m。通过二分查找,我们可以得到最小的最大分割子数组和,这样就可以得到最终的答案了。问题就可以转换为寻找最左边界的二分查找了。
1 | class Solution { |
2 | public int splitArray(int[] nums, int m) { |
3 | int low=nums[0], high=0; |
4 | for(int num : nums){ |
5 | low = Math.max(low, num); |
6 | high += num; |
7 | } |
8 | while(low <= high){ |
9 | int mid = low + (high-low)/2; |
10 | int cnt = 1; |
11 | int sum = 0; |
12 | for(int num : nums){ |
13 | if(sum + num > mid){ |
14 | cnt++; |
15 | sum = num; |
16 | }else{ |
17 | sum += num; |
18 | } |
19 | } |
20 | if(cnt > m){ |
21 | low = mid + 1; |
22 | }else{ |
23 | high = mid - 1; |
24 | } |
25 | } |
26 | return low; |
27 | } |
28 | } |
复杂度分析:
- 时间复杂度:$O(nlog(sum-max))$,$sum$是数组所有元素之和,$max$是数组中最大元素。
- 空间复杂度:$O(1)$。
附:

这也是一道二分查找题,和这题很相似,可以分析知道最小天数是0,最大天数是bloomDay数组中的最大值,如果一束花可以在第m天制作,那么在之后的天数内也可以被制作,满足单调性。因此我们可以用二分查找寻找最小制作天数。我们可以选定一个值$x$作为最后一天,然后遍历整个数组贪心的计算在第$x$天内可以制作多少束花$sum$,如果$sum<m$,那么说明在第$x$天内无法制作出要求的这么多束花,low=x+1,否则就逼近左边界high=x-1。
1 | class Solution { |
2 | public int minDays(int[] bloomDay, int m, int k) { |
3 | int low = 0; |
4 | int high = 0; |
5 | if(m*k > bloomDay.length){ |
6 | return -1; |
7 | } |
8 | for(int day : bloomDay){ |
9 | high = Math.max(high, day); |
10 | } |
11 | while(low <= high){ |
12 | int mid = low + (high-low)/2; |
13 | int cnt = getcount(bloomDay, mid, k); |
14 | if(cnt >= m){ |
15 | high = mid-1; |
16 | }else{ |
17 | low = mid+1; |
18 | } |
19 | } |
20 | return low; |
21 | } |
22 | //计算在第mid天能制作多少束花 |
23 | public int getcount(int[] bloomDay, int mid, int k){ |
24 | int count = 0; |
25 | int sum = 0; |
26 | for(int day : bloomDay){ |
27 | if(day <= mid){ |
28 | count++; |
29 | }else{ |
30 | count = 0; |
31 | } |
32 | if(count == k){ |
33 | count = 0; |
34 | sum++; |
35 | } |
36 | } |
37 | return sum; |
38 | } |
39 | } |
复杂度分析:
- 时间复杂度:$O(nlog(max))$,$max$表示花开的最大天数。
- 空间复杂度:$O(1)$。