第198场周赛
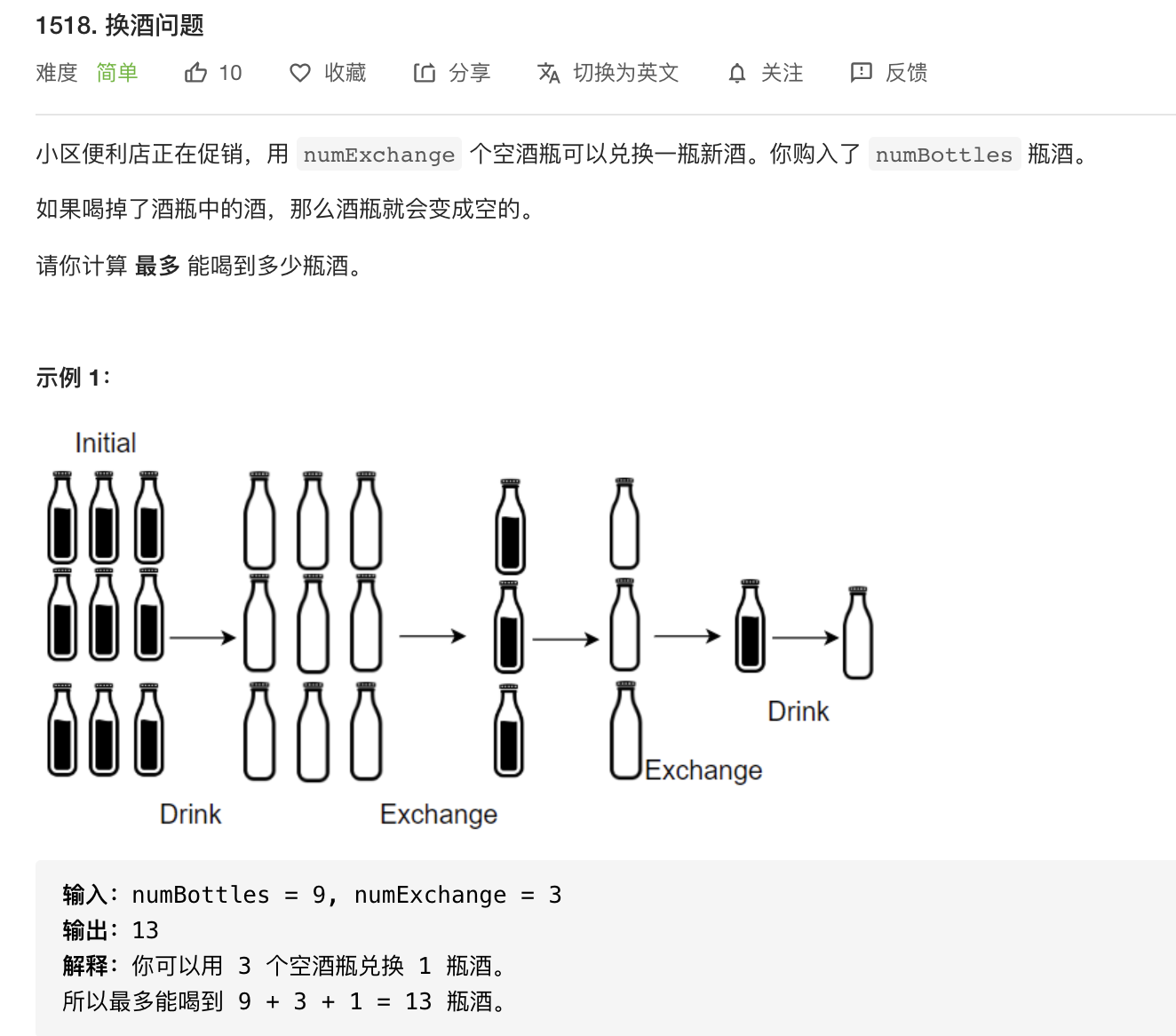
1.换酒问题
1 | class Solution { |
2 | public int numWaterBottles(int numBottles, int numExchange) { |
3 | int ans = numBottles; |
4 | int mod = 0; |
5 | while(numBottles >= numExchange){ |
6 | ans += numBottles / numExchange; |
7 | mod = numBottles % numExchange; |
8 | numBottles = numBottles / numExchange + mod; |
9 | } |
10 | return ans; |
11 | } |
12 | } |
2.子树中标签相同的节点数

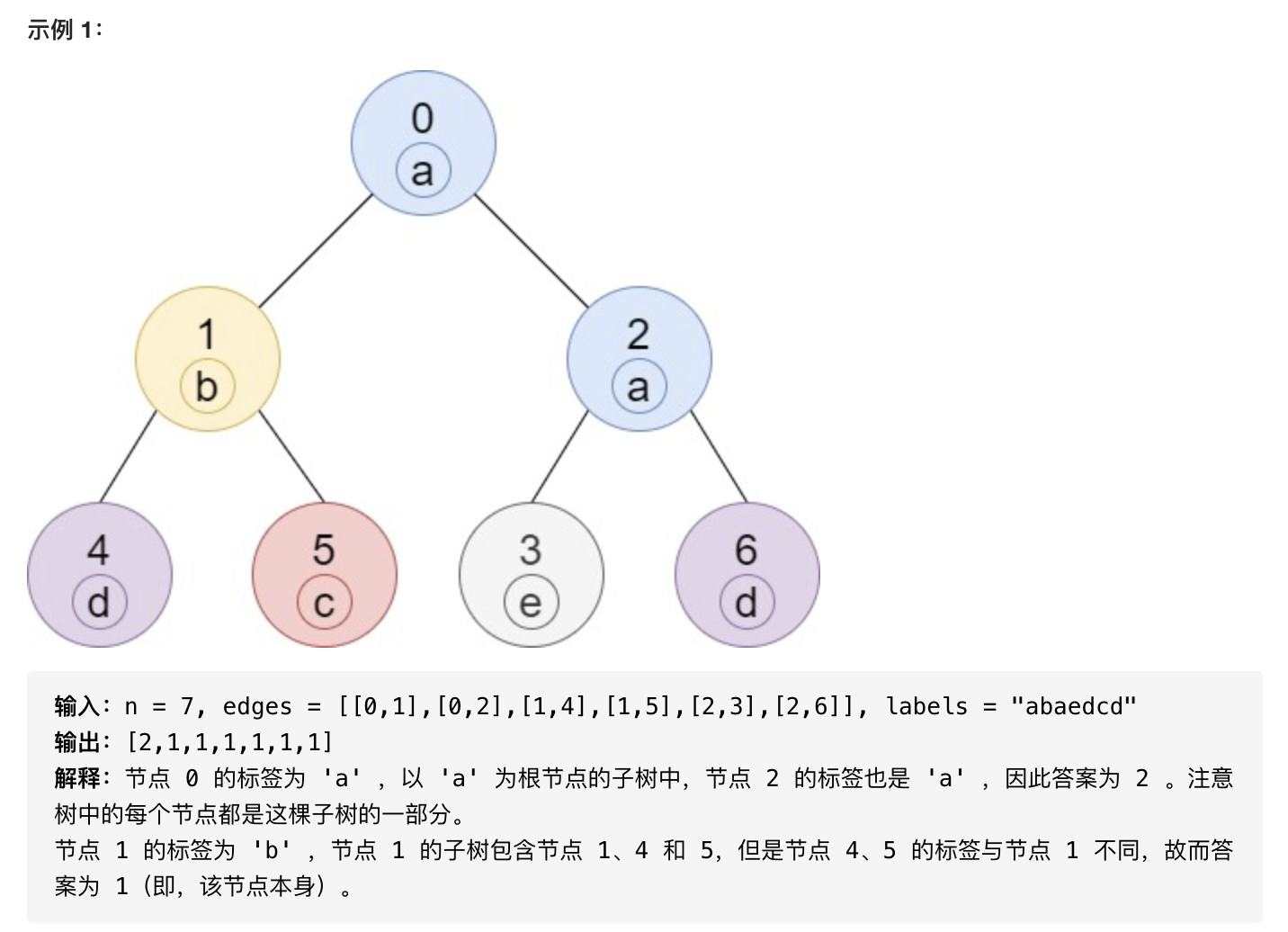
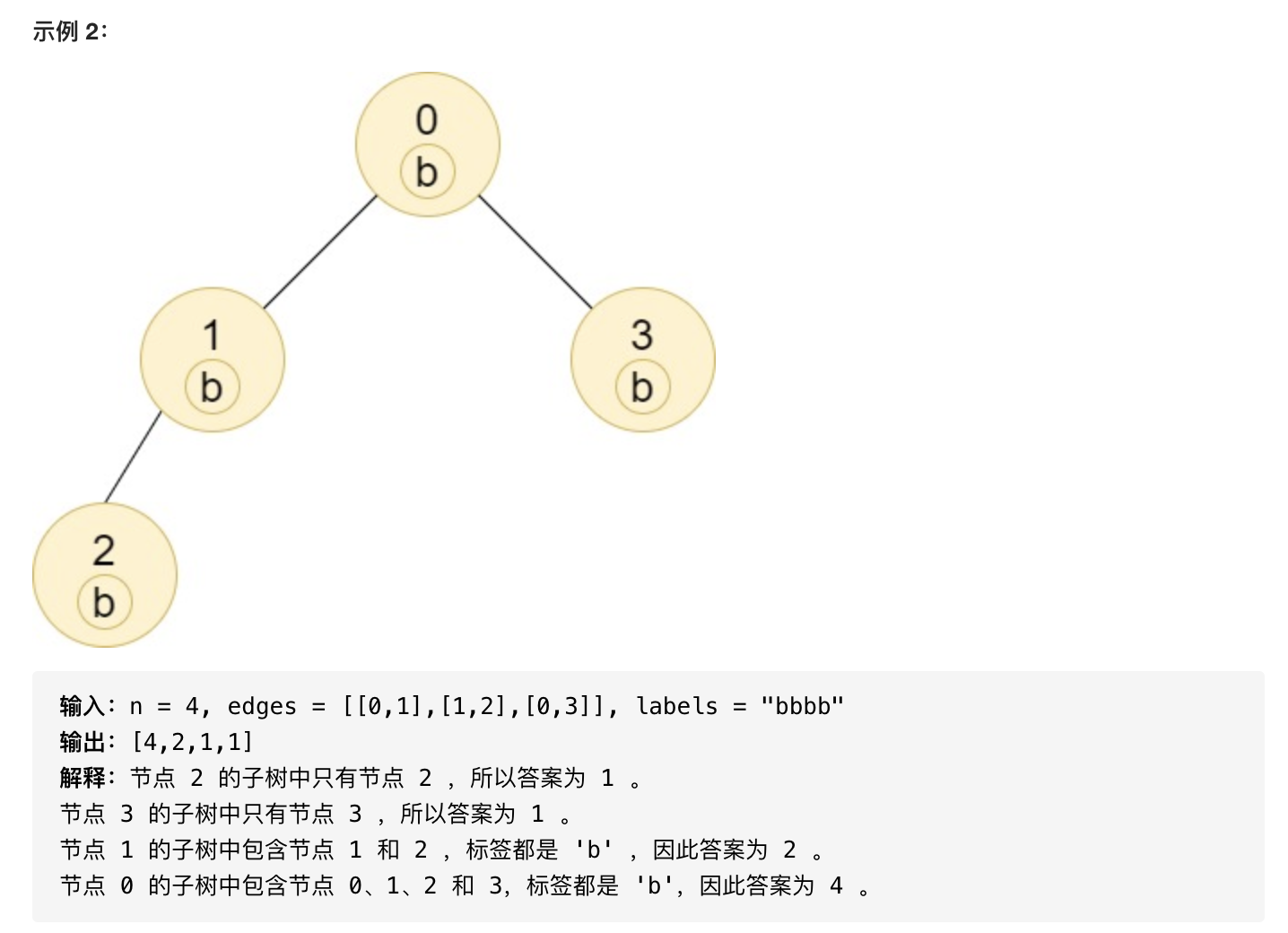
这道题需要求出每个节点的子树中与该节点标签相同的节点数,即该节点的子树中,该节点标签出现的次数。由于一个节点的子树中可能包含任意的标签,因此需要对每个节点记录该节点的子树中的所有标签的出现次数。又由于标签一定是小写字母,因此只需要对每个节点维护一个长度为 26 的数组即可。
显然,一个节点的子树中的每个标签出现的次数,由该节点的左右子树中的每个标签出现的次数以及该节点自身的标签决定,因此可以使用深度优先搜索,递归地计算每个节点的子树中的每个标签出现的次数。
当得到一个节点的子树中的每个标签出现的次数之后,即可根据该节点的标签,得到子树中与该节点标签相同的节点数。
这道题中,树的表示方法是一个连通的无环无向图。树中包含编号从 0 到 n-1 的 n 个节点,其中根节点为节点 0,以及 n-1 条无向边。由于给出的边是无向的,因此不能直接从边的节点先后顺序判断父节点和子节点。虽然给出的边是无向的,但是由于根节点已知,因此从根节点开始搜索,对每个访问到的节点标记为已访问,即可根据节点是否被访问过的信息知道相邻节点的父子关系。除了打访问标记外,还有一个办法可以解决这个问题,即在深度优先搜索的时候,把父节点当参数传入,即 dfs(now, pre, ...) 的形式,其中 now 为当前节点,pre为它的父节点,这样当邻接表中存的是无向图时,我们只要在拓展节点的时候判断 now 拓展到的节点等不等于 pre,即可避免再次拓展到父节点。
1 | class Solution { |
2 | public int[] countSubTrees(int n, int[][] edges, String labels) { |
3 | Node[] nodes = new Node[n]; |
4 | for(int i=0; i<n; i++){ |
5 | nodes[i] = new Node(); |
6 | nodes[i].c = labels.charAt(i) - 'a'; |
7 | } |
8 | for(int[] e : edges){ |
9 | Node a = nodes[e[0]]; |
10 | Node b = nodes[e[1]]; |
11 | a.adj.add(b); |
12 | b.adj.add(a); |
13 | } |
14 | dfs(nodes[0], null); |
15 | int[] ans = new int[n]; |
16 | for(int i=0; i<n; i++){ |
17 | ans[i] = nodes[i].dp[nodes[i].c]; |
18 | } |
19 | return ans; |
20 | } |
21 | |
22 | public void dfs(Node node, Node parent){ |
23 | node.dp[node.c]++; |
24 | for(Node other : node.adj){ |
25 | if(other == parent){ |
26 | continue; |
27 | } |
28 | dfs(other, node); |
29 | for(int i=0; i<='z'-'a'; i++){ |
30 | node.dp[i] += other.dp[i]; |
31 | } |
32 | } |
33 | } |
34 | } |
35 | class Node { |
36 | int c; |
37 | List<Node> adj = new ArrayList<>(); |
38 | int[] dp = new int['z' - 'a' + 1]; |
39 | } |
复杂度分析:
- 时间复杂度:$O(nc)$。其中$n$是树中的节点数,$c$是字符集大小。
- 空间复杂度:$O(nc)$。
3.最多的不重叠子字符串

1、先确定每个字母第一次出现的位置和最后出现的位置
2、若字母第一次出现的位置和最后出现的位置,中间有其他字母,并且其他字母并不全被包含在第一次出现的位置和最后出现的位置之间,则合并这两个区间
“adefaddaccc” d的第一次出现的位置和最后出现的位置之间“defadd”, 所有的e与f都在这段区间内,但a不在,合并a与d的区间
3、根据区间大小进行排序,其子区间已经被选择过,则跳过
1 | class Solution { |
2 | public List<String> maxNumOfSubstrings(String s) { |
3 | int[][] arr = new int[26][2]; |
4 | List<String> res = new ArrayList<>(); |
5 | int n = s.length(); |
6 | for(int i = 0; i < 26; i++){ |
7 | arr[i][0] = Integer.MAX_VALUE; |
8 | arr[i][1] = Integer.MAX_VALUE; |
9 | } |
10 | //最后个出现s.charAt(i)的位置 |
11 | for(int i = 0; i < n; i++){ |
12 | arr[s.charAt(i) - 'a'][1] = i; |
13 | } |
14 | //第一个出现s.charAt(i)的位置 |
15 | for(int i = n - 1; i >= 0; i--){ |
16 | arr[s.charAt(i) - 'a'][0] = i; |
17 | } |
18 | |
19 | //合并 |
20 | for(int i = 0; i < 26; i++){ |
21 | char c= (char)(i + 'a'); |
22 | if(arr[i][0] == Integer.MAX_VALUE) continue; |
23 | for(int j = arr[i][0]; j <= arr[i][1]; j++){ |
24 | if(c != s.charAt(j) && (arr[s.charAt(j) - 'a'][0] < arr[i][0] || arr[s.charAt(j) - 'a'][1] > arr[i][1])){ |
25 | arr[i][0] = Math.min(arr[i][0],arr[s.charAt(j) - 'a'][0]); |
26 | arr[i][1] = Math.max(arr[i][1],arr[s.charAt(j) - 'a'][1]); |
27 | arr[s.charAt(j) - 'a'] = arr[i]; |
28 | } |
29 | } |
30 | } |
31 | List<List<Integer>> list = new ArrayList<>(); |
32 | Set<String> set = new HashSet<>(); |
33 | |
34 | for(int i = 0; i < 26; i++){ |
35 | if(arr[i][0] == Integer.MAX_VALUE) continue; |
36 | String str = s.substring(arr[i][0],arr[i][1] + 1); |
37 | if(set.contains(str)) continue; |
38 | list.add(Arrays.asList(arr[i][0], arr[i][1])); |
39 | set.add(str); |
40 | } |
41 | |
42 | //根据长度进行排序,从短的开始选 |
43 | Collections.sort(list,((o1, o2) -> (o1.get(1)- o1.get(0))-(o2.get(1)- o2.get(0)))); |
44 | List<List<Integer>> pick = new ArrayList<>(); |
45 | for(List<Integer> tmp:list){ |
46 | boolean flag = true; |
47 | for(List<Integer> tmp2:pick){ |
48 | if(tmp2.get(0) > tmp.get(0) && tmp2.get(1) < tmp.get(1)){ |
49 | flag = false; |
50 | break; |
51 | } |
52 | } |
53 | |
54 | if(flag){ |
55 | pick.add(tmp); |
56 | res.add(s.substring(tmp.get(0),tmp.get(1) + 1)); |
57 | } |
58 | } |
59 | return res; |
60 | } |
61 | } |
复杂度分析:
- 时间复杂度:$O(n\sum + \sum log \sum)$,$n$是字符串的长度,$\sum$是字符串字符集的大小。
- 空间复杂度:$O(\sum)$。
官方题解,代码写的比较优美,比较符合java写法。
1 | class Solution { |
2 | public List<String> maxNumOfSubstrings(String s) { |
3 | Seg[] seg = new Seg[26]; |
4 | for (int i = 0; i < 26; ++i) { |
5 | seg[i] = new Seg(-1, -1); |
6 | } |
7 | // 预处理左右端点 |
8 | for (int i = 0; i < s.length(); ++i) { |
9 | int char_idx = s.charAt(i) - 'a'; |
10 | if (seg[char_idx].left == -1) { |
11 | seg[char_idx].left = seg[char_idx].right = i; |
12 | } else { |
13 | seg[char_idx].right = i; |
14 | } |
15 | } |
16 | for (int i = 0; i < 26; ++i) { |
17 | if (seg[i].left != -1) { |
18 | for (int j = seg[i].left; j <= seg[i].right; ++j) { |
19 | int char_idx = s.charAt(j) - 'a'; |
20 | if (seg[i].left <= seg[char_idx].left && seg[char_idx].right <= seg[i].right) { |
21 | continue; |
22 | } |
23 | seg[i].left = Math.min(seg[i].left, seg[char_idx].left); |
24 | seg[i].right = Math.max(seg[i].right, seg[char_idx].right); |
25 | j = seg[i].left; |
26 | } |
27 | } |
28 | } |
29 | // 贪心选取 |
30 | Arrays.sort(seg); |
31 | List<String> ans = new ArrayList<String>(); |
32 | int end = -1; |
33 | for (Seg segment : seg) { |
34 | int left = segment.left, right = segment.right; |
35 | if (left == -1) { |
36 | continue; |
37 | } |
38 | if (end == -1 || left > end) { |
39 | end = right; |
40 | ans.add(s.substring(left, right + 1)); |
41 | } |
42 | } |
43 | return ans; |
44 | } |
45 | |
46 | class Seg implements Comparable<Seg> { |
47 | int left, right; |
48 | |
49 | public Seg(int left, int right) { |
50 | this.left = left; |
51 | this.right = right; |
52 | } |
53 | |
54 | public int compareTo(Seg rhs) { |
55 | if (right == rhs.right) { |
56 | return rhs.left - left; |
57 | } |
58 | return right - rhs.right; |
59 | } |
60 | } |
61 | } |
4.找到最接近目标值的函数值
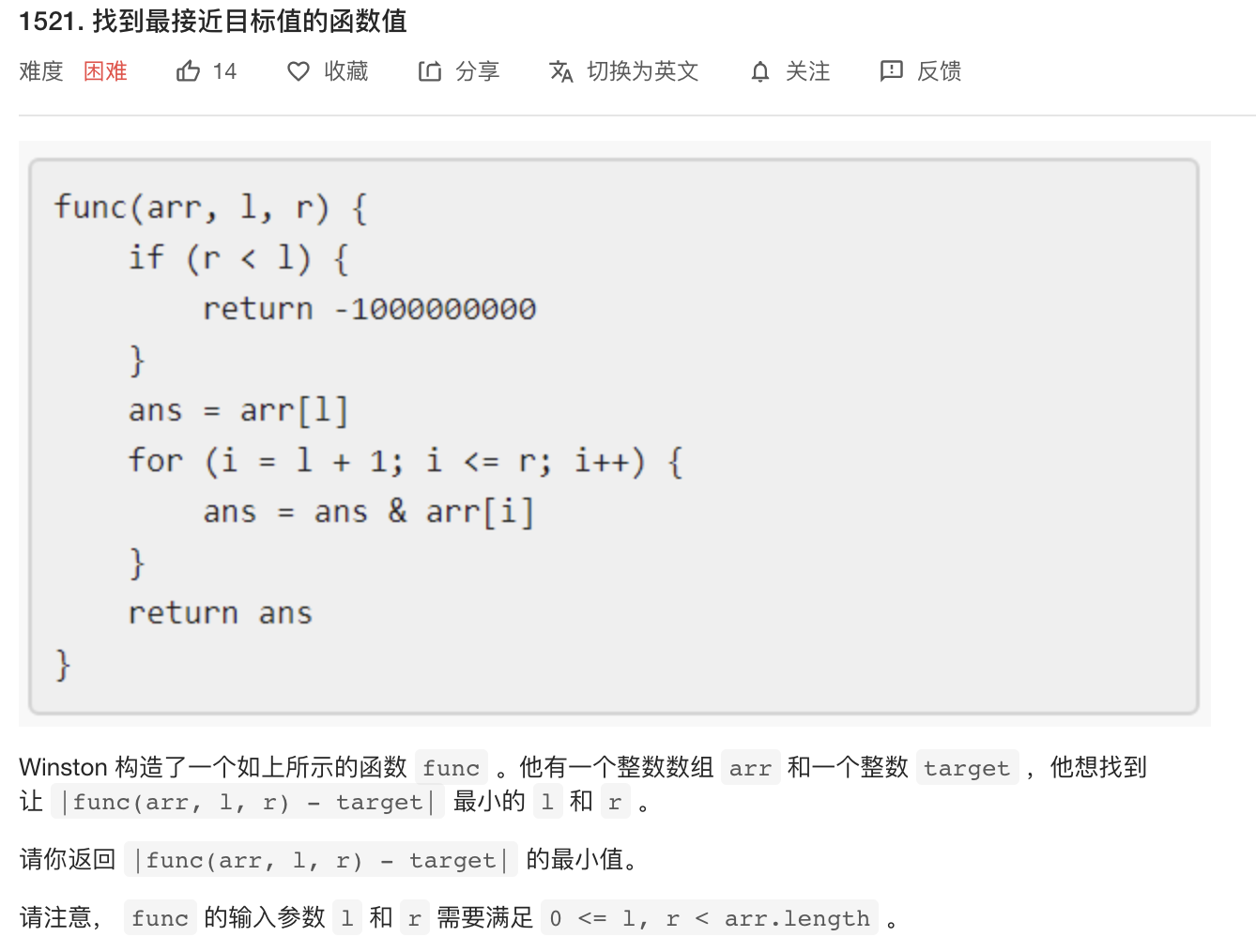

###方法一
按位与运算是题目中定义的$&$运算。按位与运算之和有以下两种性质:
如果我们固定右端点$ r$,那么左端点 $l$可以选择 $[0, r]$这个区间内的任意整数。如果我们从大到小枚举 $l$,那么:
- 按位与之和是随着 $l$的减小而单调递减的。
由于按位与运算满足结合律,所以 $func(arr,l,r)=arr[l]&func(arr,l+1,r)$。并且由于按位与运算本身的性质,$a & b$ 的值不会大于 $a$,也不会大于 $b$。因此$func(arr,l,r) <= func(arr,l+1,r)$ ,即按位与之和是随着 $l$ 的减小而单调递减的。
- 按位与之和最多只有 20 种不同的值。
当 $l=r$ 时,按位与之和就是 $arr[r]$。随着 $l$ 的减小,按位与之和变成 $arr[r−1] & arr[r]$,$arr[r−2] & arr[r−1] & arr[r]$ 等等。由于 $arr[r]≤10 ^6 <2 ^{20}$ ,那么 $arr[r]$ 的二进制表示中最多有 20 个 1。而每进行一次按位与运算,如果按位与之和发生了变化,那么值中有若干个 1 变成了 0。由于在按位与运算中,0 不能变回 1。因此值的变化的次数不会超过 $arr[r]$ 二进制表示中 1 的个数,即 $func(arr,l,r)$ 的值最多只有 20 种。
根据上面的分析,我们知道对于固定的右端点 $r$,按位与之和最多只有 20 种不同的值,因此我们可以使用一个集合维护所有的值。
我们从小到大遍历 $r$,并用一个集合实时地维护$func(arr,l,r)$ 的所有不同的值,集合的大小不过超过 20。当我们从 $r$ 遍历到 $r+1$ 时,以 $r+1$ 为右端点的值,就是集合中的每个值和 $arr[r+1]$ 进行按位与运算得到的值,再加上 $arr[r+1] $本身。我们对这些新的值进行去重,就可以得到 $func(arr,l,r+1)$ 对应的值的集合。
在遍历的过程中,当我们每次得到新的集合,就对集合中的每个值更新一次答案即可。
1 | class Solution { |
2 | public int closestToTarget(int[] arr, int target) { |
3 | int ans = Math.abs(arr[0] - target); |
4 | List<Integer> valid = new ArrayList<Integer>(); |
5 | valid.add(arr[0]); |
6 | for (int num : arr) { |
7 | List<Integer> validNew = new ArrayList<Integer>(); |
8 | validNew.add(num); |
9 | int last = num; |
10 | ans = Math.min(ans, Math.abs(num - target)); |
11 | for (int prev : valid) { |
12 | int curr = prev & num; |
13 | if (curr != last) { |
14 | validNew.add(curr); |
15 | ans = Math.min(ans, Math.abs(curr - target)); |
16 | last = curr; |
17 | } |
18 | } |
19 | valid = validNew; |
20 | } |
21 | return ans; |
22 | } |
23 | } |
复杂度分析:
- 时间复杂度:$O(nlogC)$,$C$是数组元素的最大范围。
- 空间复杂度:$O(nlogC)$。
方法二:ST表+二分
根据按位与运算的性质,我们可以知道数组按位与的结果应该是单调递减的,那么就可以用二分查找出第一个比target最小的区间数$func(arr,l,r)$,那么$func(arr,l,r-1)$就是最后一个比target大的数,之后比较这两个数与target之间的差值就可以得到结果。
那么问题就回到了如何快速的进行区间查询得到$func(arr,l,r)$的结果。可以使用线段树,时间复杂度为$O(logn)$,总体的时间复杂度就为$O(nlognlogn)$,$n$是遍历左边界,第二个$logn$是二分查找的复杂度,结果会超时。所以我们改用ST表,进行区间查询的复杂度可以降为$O(1)$,总体的时间复杂度就为$O(nlogn)$。
1 | class Solution { |
2 | public int maxn = 100005;//max(arr.length) |
3 | public int logn = 18; //log2(maxn) |
4 | public int[][] st; |
5 | public int[] Logn; |
6 | public int closestToTarget(int[] arr, int target) { |
7 | int n = arr.length; |
8 | st = new int[n][logn+1]; |
9 | Logn = new int[n+1]; |
10 | Logn[1] = 0; |
11 | Logn[2] = 1; |
12 | //存储log2的结果 |
13 | for(int i=3; i<=n; i++){ |
14 | Logn[i] = Logn[i/2] + 1; |
15 | } |
16 | //构建st表 |
17 | for(int i=0; i<n; i++){ |
18 | st[i][0] = arr[i]; |
19 | } |
20 | for(int j=1; j<=logn; j++){ |
21 | for(int i=0; i+(1<<j)-1<n; i++){ |
22 | st[i][j] = st[i][j-1] & st[i+(1<<(j-1))][j-1]; |
23 | } |
24 | } |
25 | int ans = Integer.MAX_VALUE; |
26 | //进行二分查找 |
27 | for(int left = 0; left<n; left++){ |
28 | int r_left = left+1; |
29 | int r_right = n - 1; |
30 | while(r_left <= r_right){ |
31 | int mid = r_left + (r_right-r_left)/2; |
32 | if(query(r_left,mid) >= target){ |
33 | r_left = mid+1; |
34 | }else{ |
35 | r_right = mid-1; |
36 | } |
37 | } |
38 | int right = r_right; |
39 | ans = Math.min(ans, Math.abs(target-query(left,right))); |
40 | ans = Math.min(ans, Math.abs(target-query(left,right-1))); |
41 | } |
42 | return ans; |
43 | } |
44 | public int query(int i, int j){ |
45 | if(i > j){ |
46 | return Integer.MAX_VALUE; |
47 | } |
48 | int tmp = Logn[j-i+1]; |
49 | return st[i][tmp] & st[j-(1<<tmp)+1][tmp]; |
50 | } |
51 | } |