0%

leetcode每日一题-二叉树的最大深度

Posted on In ,

二叉树的最大深度

image1

方法一：DFS递归

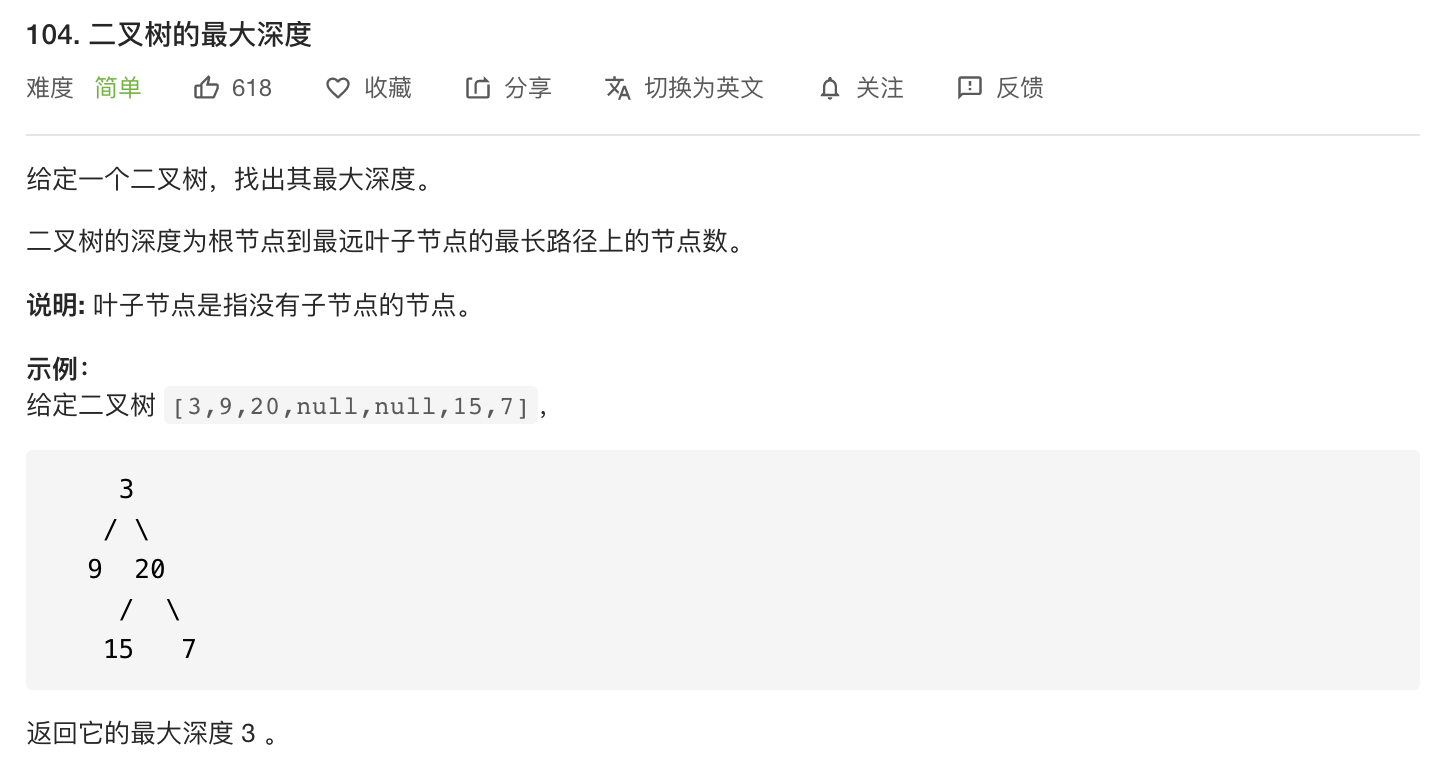
一棵二叉树的最大深度可以由左右子树的最大深度+1得到，而左右子树的最大深度又可以由它们自己的子树的最大深度得到，可以按这个思路进行递归。

1
/**
2
 * Definition for a binary tree node.
3
 * public class TreeNode {
4
 *     int val;
5
 *     TreeNode left;
6
 *     TreeNode right;
7
 *     TreeNode(int x) { val = x; }
8
 * }
9
 */
10
class Solution {
11
    public int maxDepth(TreeNode root) {
12
        if(root == null){
13
            return 0;
14
        }else{
15
            int leftdepth = maxDepth(root.left);
16
            int rightdepth = maxDepth(root.right);
17
            return Math.max(leftdepth, rightdepth)+1;
18
        }
19
    }
20
}

复杂度分析：

  • 时间复杂度：$O(n)$，其中$n$为二叉树的节点个数，每个节点在递归中被遍历一次。
  • 空间复杂度：$O(height)$，$height$表示二叉树的高度。

BFS

可以使用BFS对二叉树进行层序遍历，每遍历一层就将深度+1，因此要记录每一层的节点个数，遍历完一层就要将每一层的节点都出队列。

1
class Solution {
2
    public int maxDepth(TreeNode root) {
3
        if(root == null){
4
            return 0;
5
        }
6
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
7
        queue.offer(root);
8
        int ans = 0;
9
        while(!queue.isEmpty()){
10
            int size = queue.size();
11
            while(size > 0){
12
                TreeNode node = queue.poll();
13
                if(node.left != null){
14
                    queue.offer(node.left);
15
                }
16
                if(node.right != null){
17
                    queue.offer(node.right);
18
                }
19
                size--;
20
            }
21
            ans++;
22
        }
23
        return ans;
24
    }
25
}

复杂度分析：

  • 时间复杂度：$O(n)$。
  • 空间复杂度：$O(n)$。