课程表
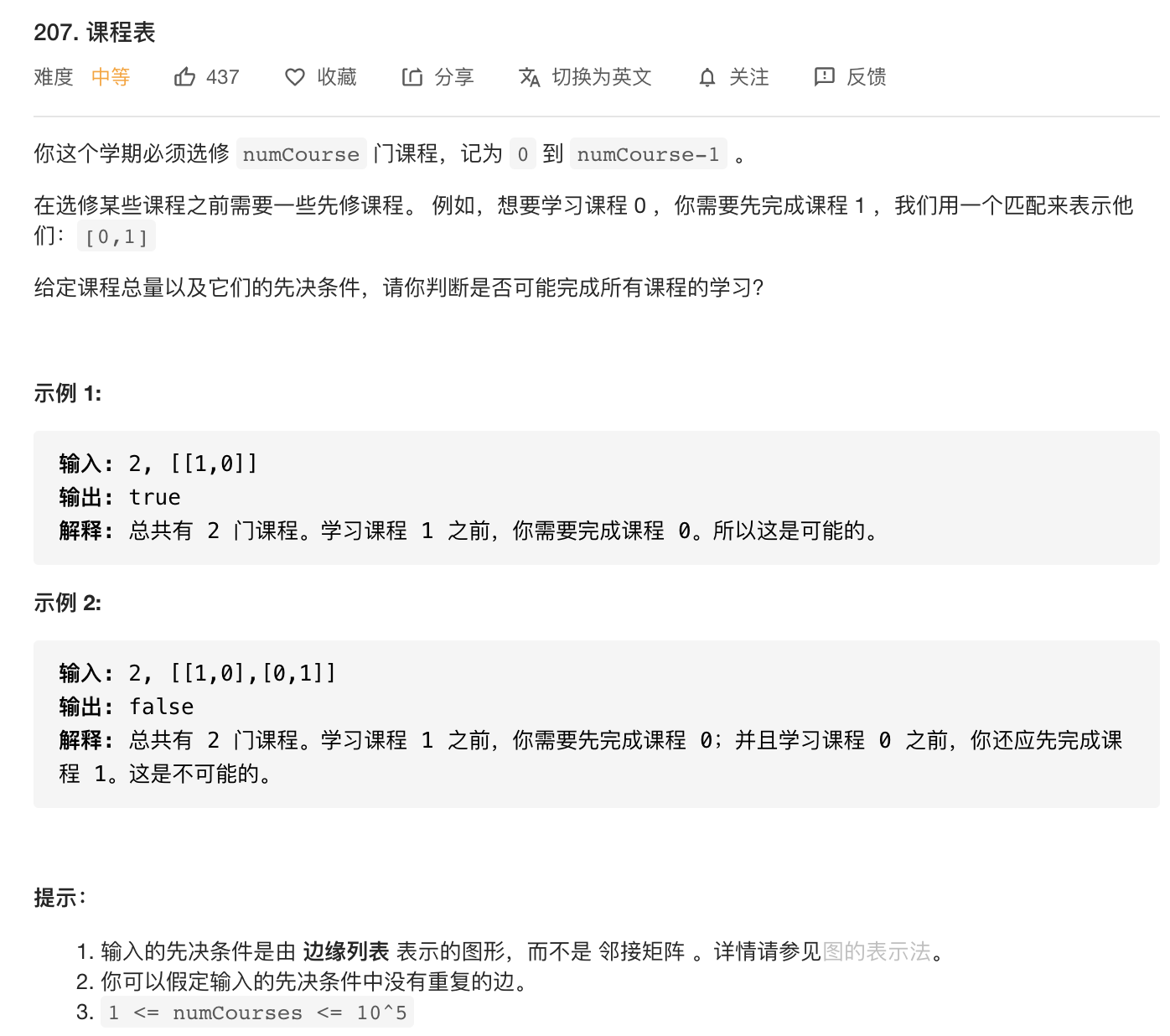
方法一:DFS
如果图中存在环,那么就无法完成所有课程的学习。我们可以用DFS来检测图中是否存在环,对于每个节点,定义三种状态,我们用flags数组来存储状态。
- 当
flags[i]==0时,说明该节点还未被访问。 - 当
flags[i]==1时,说明在本轮DFS中该节点i被第二次访问,即图中存在环,直接返回false。 - 当
flags[i]==-1时,说明该节点i已经在其他节点发起的DFS中被访问过了,无需再重复搜索,直接返回true。
1 | class Solution { |
2 | List<List<Integer>> edges; |
3 | int[] flags; |
4 | public boolean canFinish(int numCourses, int[][] prerequisites) { |
5 | edges = new ArrayList<List<Integer>>(); |
6 | for (int i = 0; i < numCourses; ++i) { |
7 | edges.add(new ArrayList<Integer>()); |
8 | } |
9 | flags = new int[numCourses]; |
10 | for(int i=0; i<prerequisites.length; i++){ |
11 | edges.get(prerequisites[i][1]).add(prerequisites[i][0]); |
12 | } |
13 | for(int i=0; i<numCourses; i++){ |
14 | if(!dfs(i)){ |
15 | return false; |
16 | } |
17 | } |
18 | return true; |
19 | |
20 | } |
21 | public boolean dfs(int index){ |
22 | if(flags[index] == 1){ |
23 | return false; |
24 | } |
25 | if(flags[index] == -1){ |
26 | return true; |
27 | } |
28 | flags[index] = 1; |
29 | List<Integer> list = edges.get(index); |
30 | for(int i=0; i<list.size(); i++){ |
31 | if(!dfs(list.get(i))){ |
32 | return false; |
33 | } |
34 | } |
35 | //回溯 |
36 | flags[index] = -1; |
37 | return true; |
38 | } |
39 | } |
复杂度分析:
- 时间复杂度:$O(m+n)$, 遍历一个图需要访问所有节点和所有临边,n 和 m 分别为节点数量和边数量;
- 空间复杂度:$O(m+n)$。
方法二:入度表BFS
可以建立一个入度表,每次选取一个入度为0的节点出队列进行BFS搜索,同时相邻节点的入度减一,如果这个过程中再出现入度为0的节点,就进队列,在这个过程中统计出队列的节点个数。最后统计出队列节点个数是否等于总的课程数,如果相等就返回true,否则说明图中有环,返回false。
1 | class Solution { |
2 | List<List<Integer>> edges; |
3 | int[] indegrees; |
4 | public boolean canFinish(int numCourses, int[][] prerequisites) { |
5 | edges = new ArrayList<List<Integer>>(); |
6 | for (int i = 0; i < numCourses; ++i) { |
7 | edges.add(new ArrayList<Integer>()); |
8 | } |
9 | indegrees = new int[numCourses]; |
10 | for(int i=0; i<prerequisites.length; i++){ |
11 | edges.get(prerequisites[i][1]).add(prerequisites[i][0]); |
12 | indegrees[prerequisites[i][0]]++; |
13 | } |
14 | Queue<Integer> queue = new LinkedList<>(); |
15 | for(int i=0; i<numCourses; i++){ |
16 | if(indegrees[i] == 0){ |
17 | queue.offer(i); |
18 | } |
19 | } |
20 | int visited = 0; |
21 | while(!queue.isEmpty()){ |
22 | int node = queue.poll(); |
23 | visited++; |
24 | List<Integer> list = edges.get(node); |
25 | for(int i=0; i<list.size(); i++){ |
26 | indegrees[list.get(i)]--; |
27 | if(indegrees[list.get(i)] == 0){ |
28 | queue.offer(list.get(i)); |
29 | } |
30 | } |
31 | } |
32 | return visited==numCourses; |
33 | } |
34 | } |
复杂度分析:
- 时间复杂度:$O(m+n)$。
- 空间复杂度:$O(m+n)$。
课程表II

这题和上面一个很相似,只不过这题要求输出拓扑排序结果。还是可以用DFS和BFS来解决。
方法一:DFS
假设我们当前搜索到了节点 u,如果它的所有相邻节点都已经搜索完成,那么这些节点都已经在栈中了,此时我们就可以把 u 入栈。可以发现,如果我们从栈顶往栈底的顺序看,由于 u 处于栈顶的位置,那么 u 出现在所有 u 的相邻节点的前面。因此对于 u 这个节点而言,它是满足拓扑排序的要求的。
这样以来,我们对图进行一遍深度优先搜索。当每个节点进行回溯的时候,我们把该节点放入栈中。最终从栈顶到栈底的序列就是一种拓扑排序。
我们可以使用数组来模拟栈。
1 | class Solution { |
2 | List<List<Integer>> edges; |
3 | int[] flags; |
4 | int[] ans; |
5 | int pos; |
6 | public int[] findOrder(int numCourses, int[][] prerequisites) { |
7 | edges = new ArrayList<List<Integer>>(); |
8 | flags = new int[numCourses]; |
9 | ans = new int[numCourses]; |
10 | pos = numCourses-1; |
11 | for(int i=0; i<numCourses; i++){ |
12 | edges.add(new ArrayList<Integer>()); |
13 | } |
14 | for(int[] info : prerequisites){ |
15 | edges.get(info[1]).add(info[0]); |
16 | } |
17 | for(int i=0; i<numCourses; i++){ |
18 | if(!dfs(i)){ |
19 | return new int[0]; |
20 | } |
21 | } |
22 | return ans; |
23 | } |
24 | public boolean dfs(int index){ |
25 | if(flags[index] == 1){ |
26 | return false; |
27 | } |
28 | if(flags[index] == -1){ |
29 | return true; |
30 | } |
31 | flags[index] = 1; |
32 | for(int node : edges.get(index)){ |
33 | if(!dfs(node)){ |
34 | return false; |
35 | } |
36 | } |
37 | flags[index] = -1; |
38 | ans[pos] = index; |
39 | pos--; |
40 | return true; |
41 | } |
42 | } |
方法二:BFS
思路和上一题一样,在每次出队列的时候记录节点即可。
1 | class Solution { |
2 | List<List<Integer>> edges; |
3 | int[] indegrees; |
4 | int[] ans; |
5 | public int[] findOrder(int numCourses, int[][] prerequisites) { |
6 | edges = new ArrayList<List<Integer>>(); |
7 | for (int i = 0; i < numCourses; ++i) { |
8 | edges.add(new ArrayList<Integer>()); |
9 | } |
10 | indegrees = new int[numCourses]; |
11 | ans = new int[numCourses]; |
12 | for(int i=0; i<prerequisites.length; i++){ |
13 | edges.get(prerequisites[i][1]).add(prerequisites[i][0]); |
14 | indegrees[prerequisites[i][0]]++; |
15 | } |
16 | Queue<Integer> queue = new LinkedList<>(); |
17 | for(int i=0; i<numCourses; i++){ |
18 | if(indegrees[i] == 0){ |
19 | queue.offer(i); |
20 | } |
21 | } |
22 | int visited = 0; |
23 | while(!queue.isEmpty()){ |
24 | int node = queue.poll(); |
25 | ans[visited++] = node; |
26 | List<Integer> list = edges.get(node); |
27 | for(int i=0; i<list.size(); i++){ |
28 | indegrees[list.get(i)]--; |
29 | if(indegrees[list.get(i)] == 0){ |
30 | queue.offer(list.get(i)); |
31 | } |
32 | } |
33 | } |
34 | if(visited!=numCourses){ |
35 | return new int[0]; |
36 | } |
37 | return ans; |
38 | } |
39 | } |