0%

leetcode每日一题-打家劫舍

Posted on In ,

打家劫舍

image1

方法一：动态规划

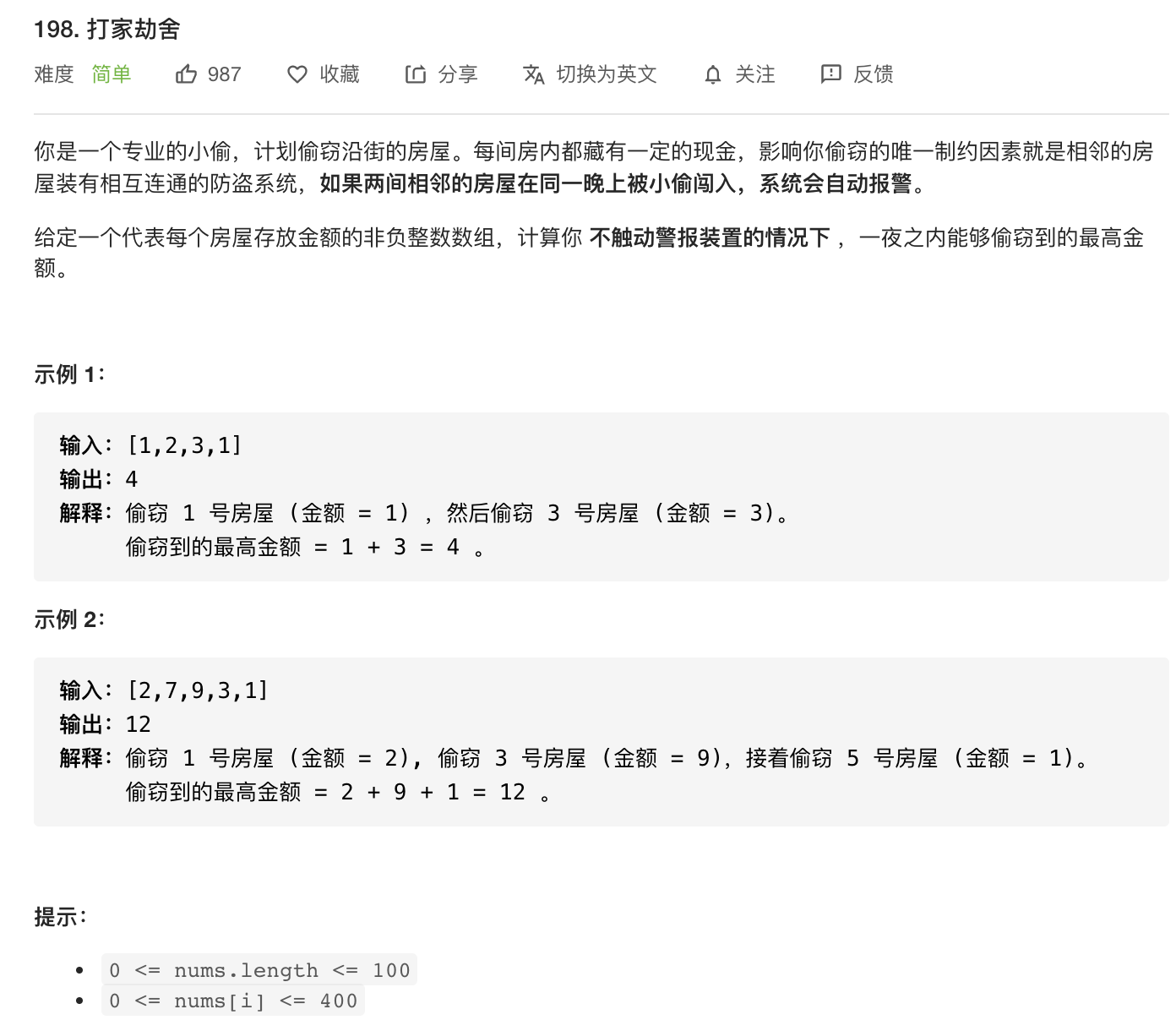
记dp[i]为第$i$天能偷到的最大金钱，那么有两种情况，第一种是第$i$天不偷钱，那么dp[i]=dp[i-1]；第二种是第$i$天偷钱，那么dp[i]=dp[i-2]+nums[i]，即前两天偷到的最大金钱加上第$i$天偷到的钱。两者取较大值。

1
class Solution {
2
    public int rob(int[] nums) {
3
        if (nums == null || nums.length == 0) {
4
            return 0;
5
        }
6
        int length = nums.length;
7
        if (length == 1) {
8
            return nums[0];
9
        }
10
        int[] dp = new int[length];
11
        dp[0] = nums[0];
12
        dp[1] = Math.max(nums[0], nums[1]);
13
        for (int i = 2; i < length; i++) {
14
            dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
15
        }
16
        return dp[length - 1];
17
    }
18
}

复杂度分析：

  • 时间复杂度：$O(n)$。
  • 空间复杂度：$O(n)$。

也可以使用滚动数组降低空间复杂度至$O(1)$。

1
class Solution {
2
    public int rob(int[] nums) {
3
        if (nums == null || nums.length == 0) {
4
            return 0;
5
        }
6
        int length = nums.length;
7
        if (length == 1) {
8
            return nums[0];
9
        }
10
        int first = nums[0], second = Math.max(nums[0], nums[1]);
11
        for (int i = 2; i < length; i++) {
12
            int temp = second;
13
            second = Math.max(first + nums[i], second);
14
            first = temp;
15
        }
16
        return second;
17
    }
18
}

打家劫舍II

image2

方法一：动态规划

还是用动态规划解决。由于头尾相连，那么可以分为两种情况，第一种是偷了第一家，也就是头，那么就只需要考虑$[1,n-1]$，最后一间房子就不需要考虑。第二种是偷了最后一家，也就是尾，那么就只需要考虑$[2,n]$，不需要考虑第一间房子。之后的步骤就和打家劫舍I一样了。

1
class Solution {
2
    public int rob(int[] nums) {
3
        if(nums.length == 0) return 0;
4
        if(nums.length == 1) return nums[0];
5
        return Math.max(myRob(Arrays.copyOfRange(nums, 0, nums.length - 1)), 
6
                        myRob(Arrays.copyOfRange(nums, 1, nums.length)));
7
    }
8
    private int myRob(int[] nums) {
9
        int pre = 0, cur = 0, tmp;
10
        for(int num : nums) {
11
            tmp = cur;
12
            cur = Math.max(pre + num, cur);
13
            pre = tmp;
14
        }
15
        return cur;
16
    }
17
}

复杂度分析：

  • 时间复杂度：$O(n)$。
  • 空间复杂度：$O(1)$。

打家劫舍III

image3

方法一：暴力递归

考虑在二叉树中存在一个爷爷，两个儿子，四个孙子。那么有两种情况，就是爷爷处得到的钱+四个孙子的钱VS两个儿子得到的钱，对于单个节点能偷的钱就是这两种情况中的较大值。

1
/**
2
 * Definition for a binary tree node.
3
 * public class TreeNode {
4
 *     int val;
5
 *     TreeNode left;
6
 *     TreeNode right;
7
 *     TreeNode(int x) { val = x; }
8
 * }
9
 */
10
class Solution {
11
    public int rob(TreeNode root) {
12
        if(root == null){
13
            return 0;
14
        }
15
        int money = root.val;
16
        if(root.left != null){
17
            money += rob(root.left.left) + rob(root.left.right);
18
        }
19
        if(root.right != null){
20
            money += rob(root.right.left) + rob(root.right.right);
21
        }
22
        money = Math.max(money, rob(root.left)+rob(root.right));
23
        return money;
24
    }
25
}

复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(1)$

方法二：记忆化搜索

在方法一中，在计算单个节点得到的钱时，会有重复计算，所以我们可以用一个哈希表来记录单个节点得到的钱，省去了重复计算。

1
class Solution {
2
    Map<TreeNode, Integer> memo;
3
    public int rob(TreeNode root) {
4
        memo = new HashMap<TreeNode, Integer>();
5
        return robSearch(root);
6
    }
7
8
    public int robSearch(TreeNode root){
9
        if(root == null) return 0;
10
        if(memo.containsKey(root)) return memo.get(root);
11
        int money = root.val;
12
        if(root.left != null){
13
            money += robSearch(root.left.left) + robSearch(root.left.right);
14
        }
15
        if(root.right != null){
16
            money += robSearch(root.right.left) + robSearch(root.right.right);
17
        }
18
        money = Math.max(money, robSearch(root.left)+robSearch(root.right));
19
        memo.put(root, money);
20
        return money;
21
    }
22
}

复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

方法三：动态规划

我们使用一个大小为 2 的数组来表示 int[] res = new int[2] 0 代表不偷，1 代表偷
任何一个节点能偷到的最大钱的状态可以定义为

  1. 当前节点选择不偷：当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱

  2. 当前节点选择偷：当前节点能偷到的最大钱数 = 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱 + 当前节点的钱数

1
class Solution {
2
    public int rob(TreeNode root) {
3
        int[] result = robSearch(root);
4
        return Math.max(result[0], result[1]);
5
    }
6
7
    public int[] robSearch(TreeNode root){
8
        if(root == null) return new int[2];
9
        int[] money = new int[2];
10
        int[] left = robSearch(root.left);
11
        int[] right = robSearch(root.right);
12
13
        money[0] = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);
14
        money[1] = left[0] + right[0] + root.val;
15
        return money;
16
    }
17
}

复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$