0%

leetcode每日一题-被围绕的区域

Posted on In ,

被围绕的区域

image1

方法一：深度优先搜索

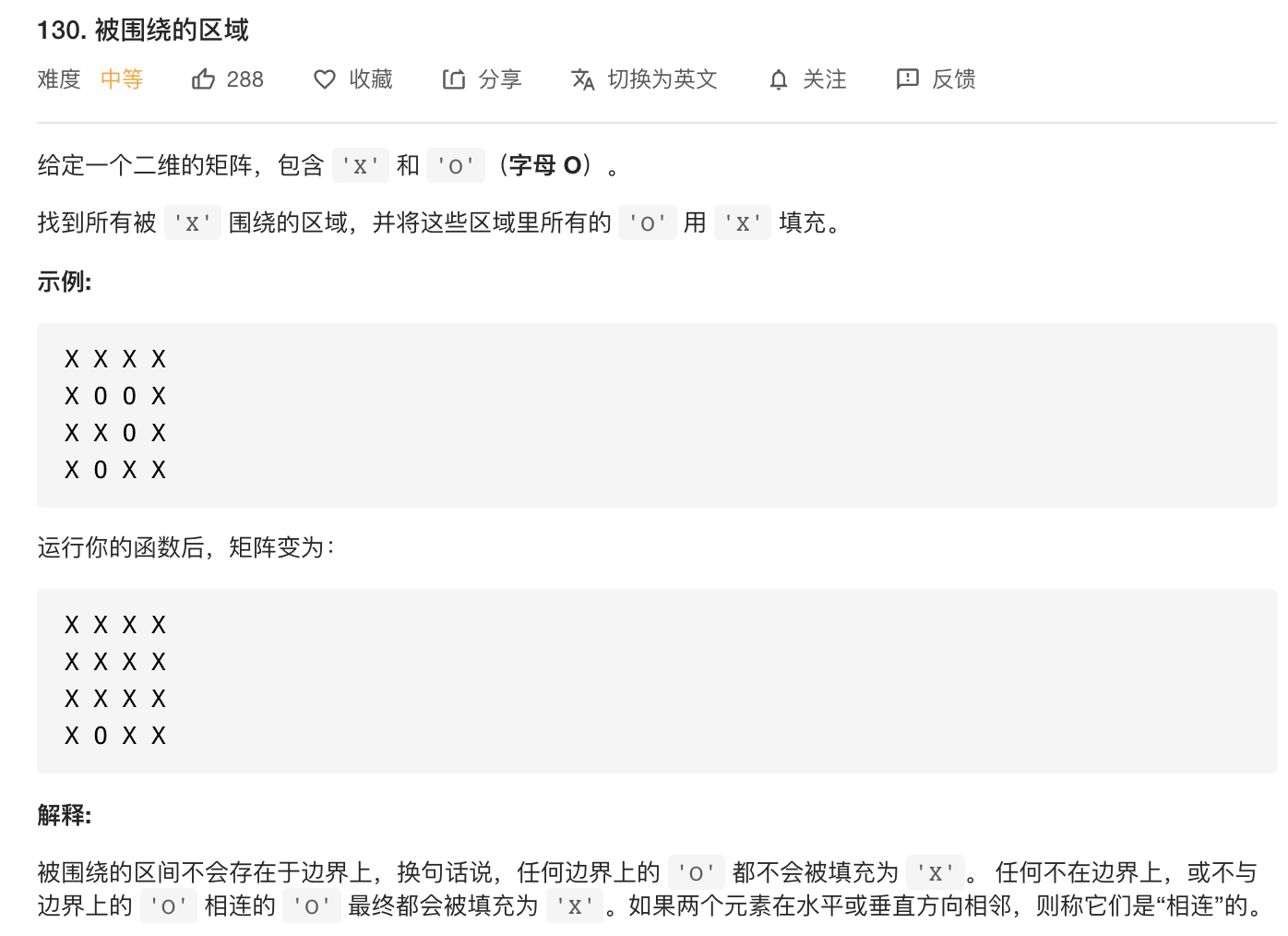
根据题意我们可以知道如果某一个O与边界上的O相连通，那么这个O就不属于被围绕的区域，不能被填充为X。因此我们只需要找出所有与边界上的O相连通的O。那么可以从某个边界上的O出发进行DFS。我们使用一个二维标记数组flag[i][j]来标记board[i][j]是否与边界上的O连通，true表示连通，不需要填充为X。再使用一个二维数组visited[i][j]来标记board[i][j]在DFS时候是否被访问过，避免重复访问陷入死循环。

1
class Solution {
2
    int m, n;
3
    boolean[][] flag;
4
    boolean[][] visited;
5
    public void solve(char[][] board) {
6
        if(board==null || board.length==0){
7
            return;
8
        }
9
        m = board.length;
10
        n = board[0].length;
11
        flag = new boolean[m][n];
12
        visited = new boolean[m][n];
13
        for(int i=0; i<m; i++){
14
            for(int j=0; j<n; j++){
15
                if(board[i][j] == 'O' && (i==m-1||i==0 || j==n-1||j==0)){ 
16
                    flag[i][j] = true;
17
                    visited[i][j] = true;
18
                    dfs(board, i, j);
19
                }
20
            }
21
        }
22
        for(int i=0; i<m; i++){
23
            for(int j=0; j<n; j++){
24
                if(board[i][j] == 'O' && !flag[i][j]){
25
                    board[i][j] = 'X';
26
                }
27
            }
28
        }
29
    }
30
31
    public void dfs(char[][] board, int row, int col){
32
        visited[row][col] = true;
33
        if(col+1<n && board[row][col+1]=='O' && !visited[row][col+1]){
34
            dfs(board, row, col+1);
35
        }
36
        if(col-1>=0 && board[row][col-1]=='O' && !visited[row][col-1]){
37
            dfs(board, row, col-1);
38
        }
39
        if(row-1>=0 && board[row-1][col]=='O' && !visited[row-1][col]){
40
            dfs(board, row-1, col);
41
        }
42
        if(row+1<m && board[row+1][col]=='O' && !visited[row+1][col]){
43
            dfs(board, row+1, col);
44
        }
45
        flag[row][col] = true;
46
    }
47
}

我们也可以优化一下此代码，避免开辟额外的空间存储flag和visited，思路是在进行DFS过程中，如果某处O与边界的O相连通，就将O改写为A，之后在遍历过程中，将A都改写为O，将未改写的O填充为X，这样就避免了额外开辟数组。

1
class Solution {
2
    int m, n;
3
    public void solve(char[][] board) {
4
        if(board==null || board.length==0){
5
            return;
6
        }
7
        m = board.length;
8
        n = board[0].length;
9
        for(int i=0; i<m; i++){
10
            for(int j=0; j<n; j++){
11
                if(i==m-1 || i==0 || j==n-1 || j==0){ 
12
                    dfs(board, i, j);
13
                }
14
            }
15
        }
16
        for(int i=0; i<m; i++){
17
            for(int j=0; j<n; j++){
18
                if(board[i][j] == 'A'){
19
                    board[i][j] = 'O';
20
                }else if(board[i][j] == 'O'){
21
                    board[i][j] = 'X';
22
                }
23
            }
24
        }
25
    }
26
27
    public void dfs(char[][] board, int x, int y){
28
        if(x<0 || x>=m || y<0 || y>=n || board[x][y]!='O'){
29
            return;
30
        }
31
        board[x][y] = 'A';
32
        dfs(board, x-1, y);
33
        dfs(board, x+1, y);
34
        dfs(board, x, y+1);
35
        dfs(board, x, y-1);
36
    }
37
}

复杂度分析：

  • 时间复杂度：$O(m \times n)$
  • 空间复杂度：$O(m \times n)$，主要是深搜时栈的开销。

方法二：广度优先搜索

我们也可以用广度优先搜索与边界O相连通的区域。

1
class Solution {
2
    int[] dx = {-1, 1, 0, 0};
3
    int[] dy = {0, 0, -1, 1};
4
    public void solve(char[][] board) {
5
        if(board==null || board.length==0){
6
            return;
7
        }
8
        int m = board.length;
9
        int n = board[0].length;
10
        Queue<int[]> queue = new LinkedList<int[]>();
11
        for(int i=0; i<m; i++){
12
            for(int j=0; j<n; j++){
13
                if((i==m-1 || i==0 || j==n-1 || j==0) && board[i][j]=='O'){
14
                    queue.offer(new int[]{i,j});             
15
                }
16
            }
17
        }
18
        while(!queue.isEmpty()){
19
            int[] cell = queue.poll();
20
            board[cell[0]][cell[1]] = 'A';
21
            for(int i=0; i<4; i++){
22
                int x = cell[0] + dx[i];
23
                int y = cell[1] + dy[i];
24
                if(x<0 || x>=m || y<0 || y>=n || board[x][y]!='O'){
25
                    continue;
26
                }
27
                queue.offer(new int[]{x,y});
28
            }
29
        }
30
        for(int i=0; i<m; i++){
31
            for(int j=0; j<n; j++){
32
                if(board[i][j] == 'A'){
33
                    board[i][j] = 'O';
34
                }else if(board[i][j] == 'O'){
35
                    board[i][j] = 'X';
36
                }
37
            }
38
        }
39
    }
40
}

复杂度分析：

  • 时间复杂度：$O(m \times n)$
  • 空间复杂度：$O(m \times n)$，主要是广搜时队列的开销。