0%

leetcode每日一题-克隆图

Posted on In ,

克隆图

image1

image2

image3

方法一：广度优先搜索

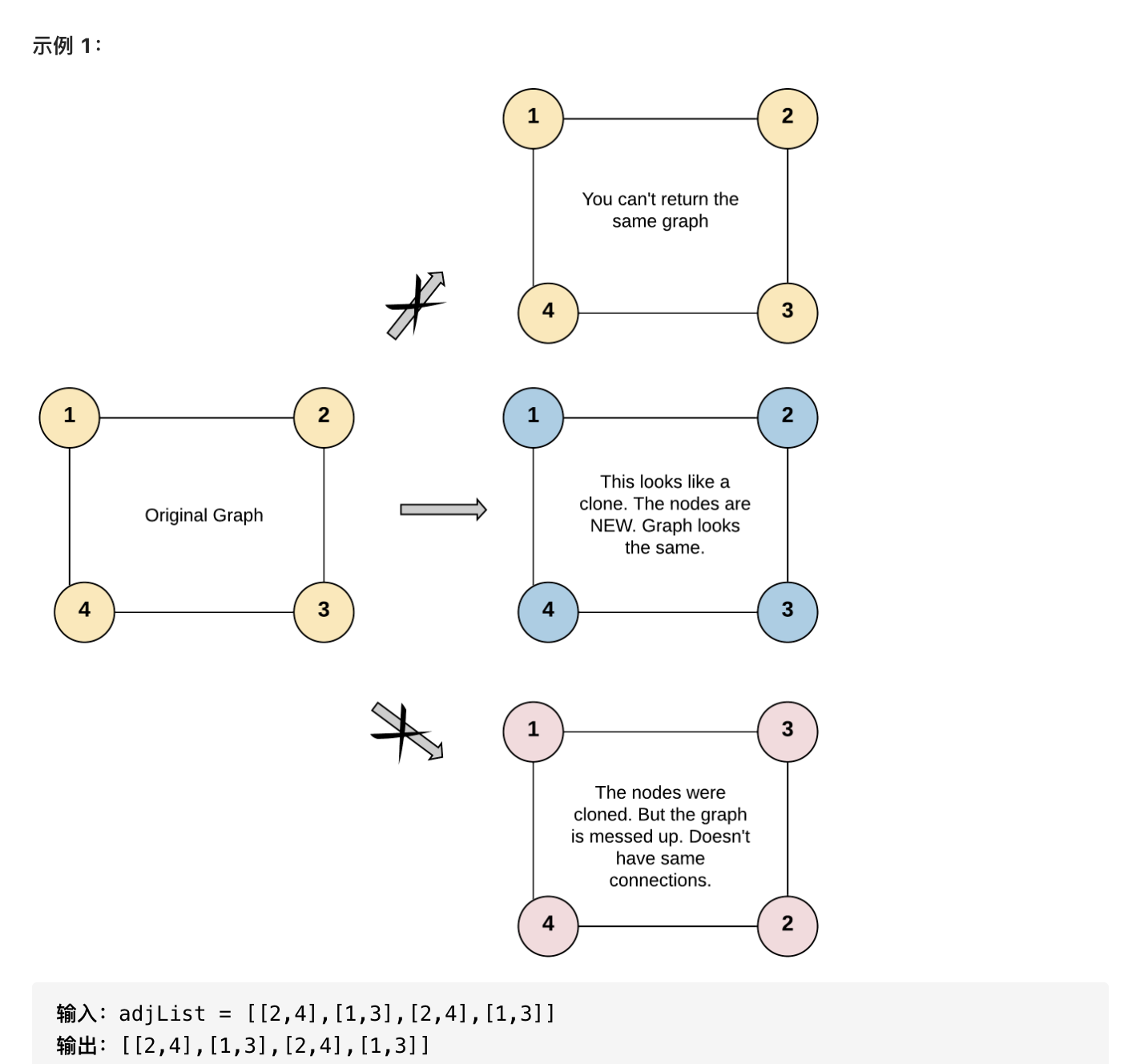
先用BFS遍历一遍图，在遍历过程中克隆节点，用哈希表存储每个节点对应的克隆节点。再进行一次遍历，在第二次遍历过程中创建每个克隆节点的邻接表。

1
/*
2
// Definition for a Node.
3
class Node {
4
    public int val;
5
    public List<Node> neighbors;
6
    
7
    public Node() {
8
        val = 0;
9
        neighbors = new ArrayList<Node>();
10
    }
11
    
12
    public Node(int _val) {
13
        val = _val;
14
        neighbors = new ArrayList<Node>();
15
    }
16
    
17
    public Node(int _val, ArrayList<Node> _neighbors) {
18
        val = _val;
19
        neighbors = _neighbors;
20
    }
21
}
22
*/
23
24
class Solution {
25
    public Node cloneGraph(Node node) {
26
        if(node == null){
27
            return null;
28
        }
29
        Queue<Node> queue = new LinkedList<Node>();
30
        Map<Integer, Node> map = new HashMap<Integer, Node>();
31
        queue.offer(node);
32
        while(!queue.isEmpty()){
33
            Node cur = queue.poll();
34
            map.put(cur.val, new Node(cur.val));
35
            for(Node n : cur.neighbors){
36
                if(!map.containsKey(n.val)){
37
                    queue.offer(n);
38
                }
39
            }
40
        }
41
        queue.offer(node);
42
        boolean[] visited = new boolean[map.size()+1];
43
        while(!queue.isEmpty()){
44
            Node cur = queue.poll();
45
            visited[cur.val] = true;
46
            Node p = map.get(cur.val);
47
            for(Node n : cur.neighbors){
48
                p.neighbors.add(map.get(n.val));
49
                if(!visited[n.val]){
50
                    queue.offer(n);
51
                    visited[n.val] = true;
52
                }
53
            }
54
        }
55
        return map.getOrDefault(node.val, new Node());
56
    }
57
}

可以进行优化，即在第一遍BFS的时候就添加邻接表。方法就是创建一个Map<Node, Node>的哈希表，记录原节点与克隆节点对应关系。在访问某个节点的邻接表时，如果邻居对应的克隆节点不存在，那么就先创建，之后再将创建的克隆节点加入自身对应克隆节点的邻接表中。

1
class Solution {
2
    public Node cloneGraph(Node node) {
3
        if(node == null){
4
            return null;
5
        }
6
      	// 将题目给定的节点添加到队列
7
        Queue<Node> queue = new LinkedList<Node>();
8
        Map<Node, Node> map = new HashMap<Node, Node>();
9
      	// 克隆第一个节点并存储到哈希表中
10
        map.put(node, new Node(node.val));
11
        queue.offer(node);
12
      	// 广度优先搜索
13
        while(!queue.isEmpty()){
14
          	// 取出队列的头节点
15
            Node cur = queue.poll();
16
          	// 遍历该节点的邻居
17
            for(Node n : cur.neighbors){
18
                if(!map.containsKey(n)){
19
                  	// 如果没有被访问过，就克隆并存储在哈希表中
20
                    map.put(n, new Node(n.val));
21
                  	// 将邻居节点加入队列中
22
                    queue.offer(n);
23
                }
24
              	// 更新当前节点的邻居列表
25
                map.get(cur).neighbors.add(map.get(n));
26
            }
27
        }
28
        return map.getOrDefault(node, new Node());
29
    }
30
}

复杂度分析：

  • 时间复杂度：$O(n)$，$n$是节点数量。
  • 空间复杂度：$O(n)$。

方法二：深度优先搜索

同样使用哈希表来存储原节点与克隆节点的对应关系，如果当前访问的节点不在哈希表中，则创建它的克隆节点并存储在哈希表中。注意：在进入递归之前，必须先创建克隆节点并保存在哈希表中。如果不保证这种顺序，可能会在递归中再次遇到同一个节点，再次遍历该节点时，陷入死循环。递归调用每个节点的邻接点。每个节点递归调用的次数等于邻接点的数量，每一次调用返回其对应邻接点的克隆节点，最终返回这些克隆邻接点的列表，将其放入对应克隆节点的邻接表中。这样就可以克隆给定的节点和其邻接点。

1
class Solution {
2
    Map<Node, Node> map = new HashMap<Node, Node>();
3
    public Node cloneGraph(Node node) {
4
        if(node == null){
5
            return null;
6
        }
7
        // 如果该节点已经被访问过了，则直接从哈希表中取出对应的克隆节点返回
8
        if(map.containsKey(node)){
9
            return map.get(node);
10
        }
11
        // 克隆节点，注意到为了深拷贝我们不会克隆它的邻居的列表
12
        Node cloneNode = new Node(node.val);
13
        // 哈希表存储
14
        map.put(node, cloneNode);
15
        // 遍历该节点的邻居并更新克隆节点的邻居列表
16
        for(Node neighbor : node.neighbors){
17
            cloneNode.neighbors.add(cloneGraph(neighbor));
18
        }
19
        return cloneNode;
20
    }
21
}

复杂度分析：

  • 时间复杂度：$O(n)$。
  • 空间复杂度：$O(n)$。