0%

leetcode每日一题-扫雷游戏

Posted on In ,

扫雷游戏

image1

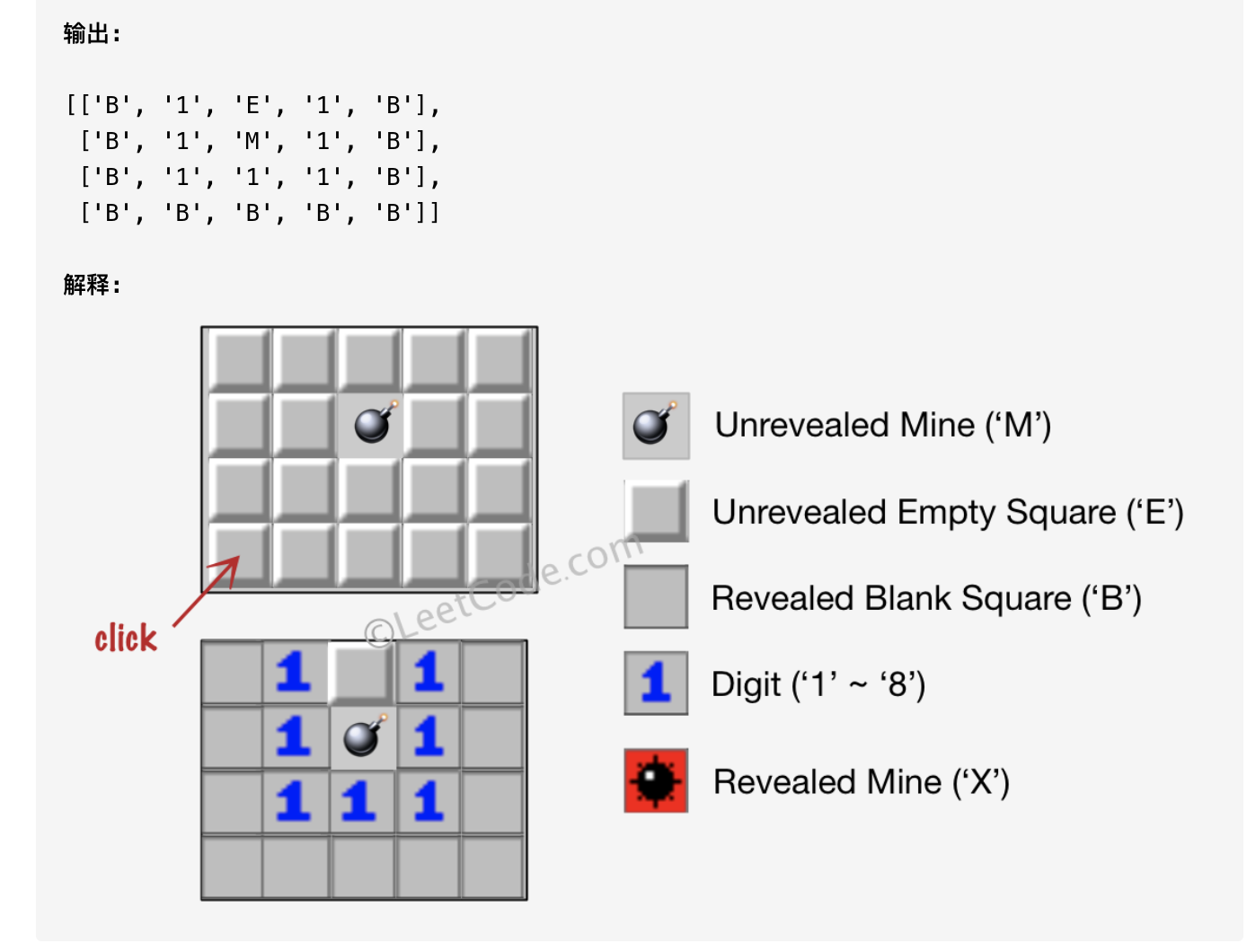
image2

image3

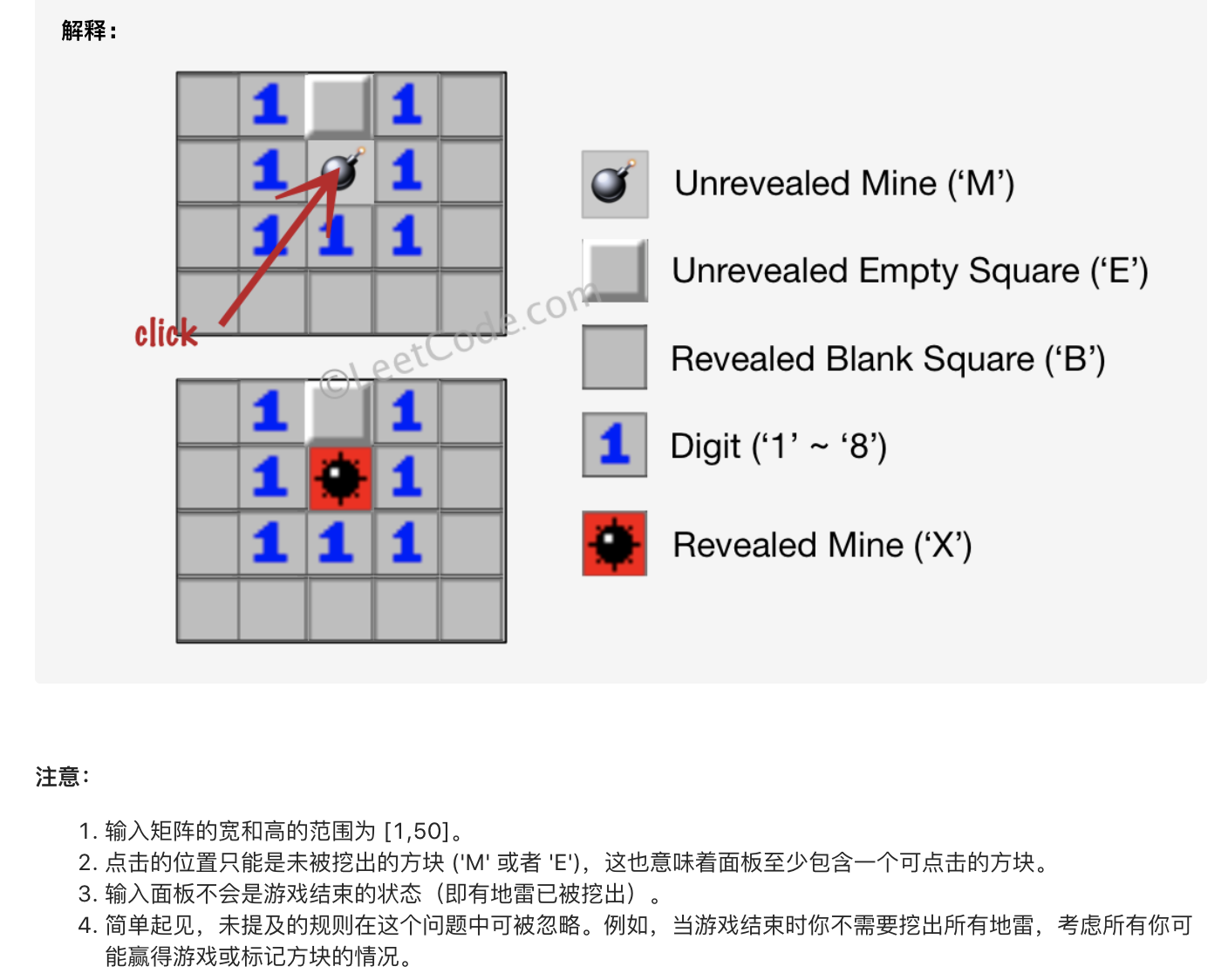
image4

方法一：深度优先搜索

  1. 如果当前点击的是地雷，直接将其修改为$X$即可。
  2. 如果当前点击未挖出的空方块，那么就先统计该方块周围的地雷数，如果地雷数不为0，那么就将当前空方块改为数字，否则就将该空方块改为$B$，之后继续搜索递归处理周围为$E$的空方块。搜索过程可以使用深度优先搜索。
1
class Solution {
2
    int[] dx = {-1,1,0,0,-1,-1,1,1};
3
    int[] dy = {0,0,1,-1,1,-1,1,-1};
4
    int m, n;
5
    public char[][] updateBoard(char[][] board, int[] click) {
6
        if(board[click[0]][click[1]] == 'M'){
7
            board[click[0]][click[1]] = 'X';
8
            return board;
9
        }else{
10
            m = board.length;
11
            n = board[0].length;
12
            dfs(board, click[0], click[1]);
13
        }
14
        return board;
15
    }
16
17
    public void dfs(char[][] board, int x, int y){
18
        int count = 0;
19
        for(int i=0; i<8; i++){
20
            int mx = x + dx[i];
21
            int my = y + dy[i];
22
            if(mx>=0 && mx<m && my>=0 && my<n && board[mx][my]=='M'){
23
                count++;
24
            }
25
        }
26
        if(count > 0){
27
            board[x][y] = (char)(count + '0');
28
        }else{
29
            board[x][y] = 'B';
30
            for(int i=0; i<8; i++){
31
                int mx = x + dx[i];
32
                int my = y + dy[i];
33
                if(mx>=0 && mx<m && my>=0 && my<n && board[mx][my]=='E'){
34
                    dfs(board, mx, my);
35
                }
36
            }
37
        }
38
    }
39
}

复杂度分析：

  • 时间复杂度：$O(mn)$。
  • 空间复杂度：$O(mn)$。

方法二：广度优先搜索

上面第二种情况的搜索可以用广度优先搜索，但是需要另外一个visited数组来记录访问过的方块避免重复访问。

1
class Solution {
2
    int[] dx = {-1,1,0,0,-1,-1,1,1};
3
    int[] dy = {0,0,1,-1,1,-1,1,-1};
4
    boolean[][] visited;
5
    public char[][] updateBoard(char[][] board, int[] click) {
6
        if(board[click[0]][click[1]] == 'M'){
7
            board[click[0]][click[1]] = 'X';
8
            return board;
9
        }
10
        int m = board.length;
11
        int n = board[0].length;
12
        visited = new boolean[m][n];
13
        Queue<int[]> queue = new LinkedList<int[]>();
14
        queue.offer(click);
15
        visited[click[0]][click[1]] = true;
16
        while(!queue.isEmpty()){
17
            int[] cur = queue.poll();
18
            int x = cur[0];
19
            int y = cur[1];
20
            if(board[x][y] == 'M'){
21
                continue;
22
            }
23
            int count = 0;
24
            for(int i=0; i<8; i++){
25
                int mx = x + dx[i];
26
                int my = y + dy[i];
27
                if(mx<m && mx>=0 && my<n && my>=0 && board[mx][my]=='M'){
28
                    count++;
29
                }
30
            }
31
            if(count == 0){
32
                board[x][y] = 'B';
33
                for(int i=0; i<8; i++){
34
                    int mx = x + dx[i];
35
                    int my = y + dy[i];
36
                    if(mx<m && mx>=0 && my<n && my>=0 && !visited[mx][my]){
37
                        queue.offer(new int[]{mx,my});
38
                        visited[mx][my] = true;
39
                    }
40
                }
41
            }else{
42
                board[x][y] = (char)(count+'0');
43
            }
44
        }
45
        return board;
46
47
    }
48
}

复杂度分析：

  • 时间复杂度：$O(mn)$。
  • 空间复杂度：$O(mn)$。