0%

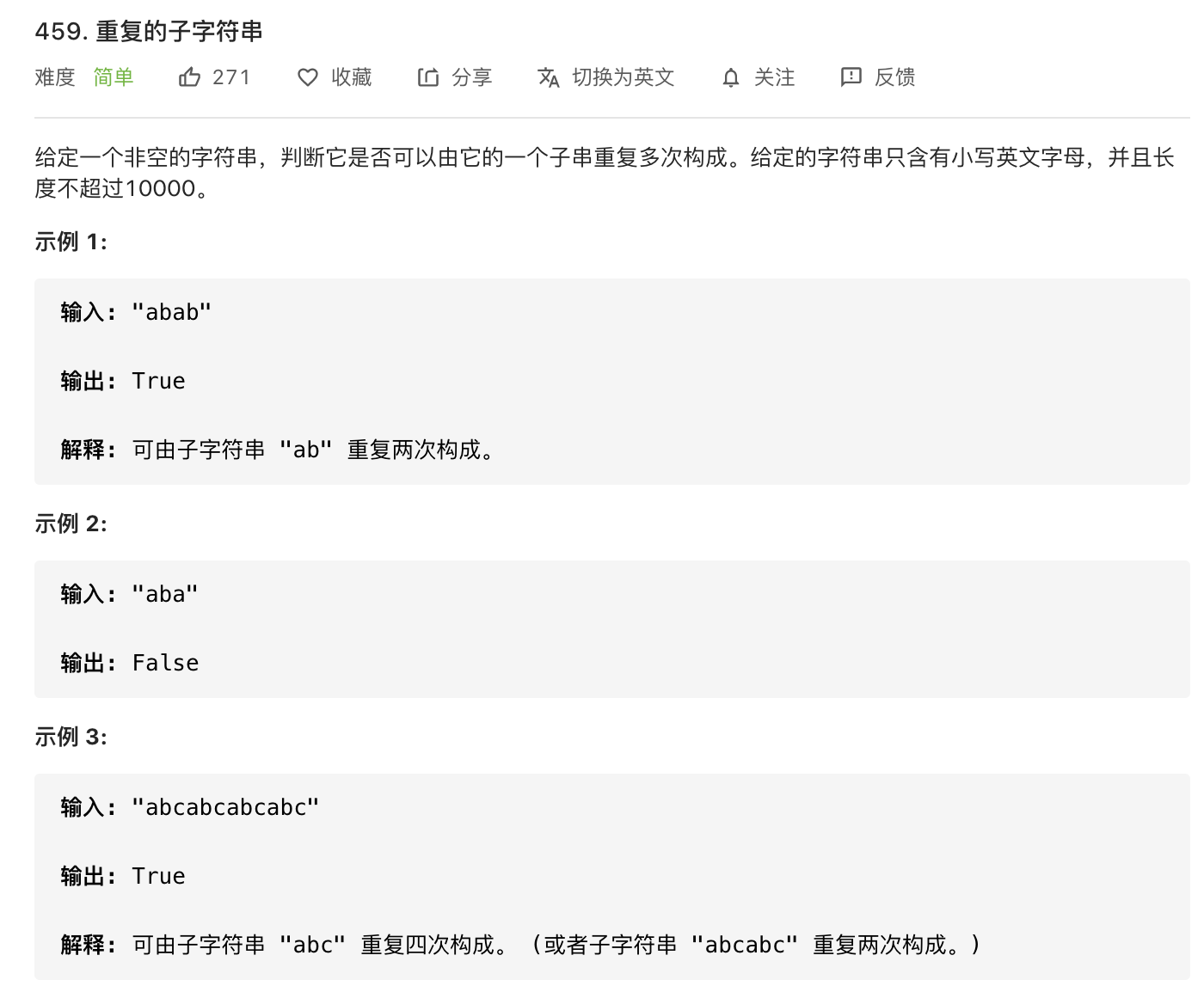
leetcode每日一题-重复的子字符串

Posted on In ,

重复的子字符串

image1

方法一：枚举

从小到大枚举s的前缀字符串$s’ = s[0:i]$，再判断s是否由$s’$重复构成。注意$s’$长度不会超过s的一半。

1
class Solution {
2
    public boolean repeatedSubstringPattern(String s) {
3
        if(s==null || s.length()==1){
4
            return false;
5
        }
6
        int len = s.length();
7
        for(int i=0; i<len/2; i++){
8
            int sublen = i+1;
9
            if(len%sublen != 0 ){
10
                continue;
11
            }
12
            String sub = s.substring(0, sublen);
13
            boolean flag = true;
14
            for(int j=1; j<len/sublen; j++){
15
                if(!sub.equals(s.substring(j*sublen, (j+1)*sublen))){
16
                    flag = false;
17
                }
18
            }
19
            if(flag){
20
                return true;
21
            }
22
        }
23
        return false;
24
    }
25
}

复杂度分析：

  • 时间复杂度：$O(n^2)$。
  • 空间复杂度：$O(1)$。

方法二：字符串匹配

假设s满足题意，那么我们可以把s写成$s=s’s’s’…s’$的形式，那么如果将两个s前后连起来，排除ss的第一个字符和最后一个字符，在新的字符串ss中去寻找s，即在$ss[1:2n-2]$中去匹配s，如果s满足题意，那么s就肯定是$ss[1:2n-2]$的子串，否则不是。以$s=”abab”$为例，那么$ss=”abababab”$，$ss[1:2n-2]=”bababa”$，那么s是其中一个子串，反例考虑$s=”aba”$，那么$ss[1:2n-2]=”baab”$，可见s并非其中的一个子串。

1
class Solution {
2
    public boolean repeatedSubstringPattern(String s) {
3
        return (s+s).indexOf(s, 1) != s.length();
4
    }
5
}

方法三：KMP算法

在方法二中，我们使用了语言自带的字符串查找函数。同样我们也可以自己实现这个函数，例如使用比较经典的 KMP 算法。其中$fail[i]$数组的作用是找出模式串$s[0:i-1]$的最长的公共前后缀，关于$fail$数组的实现，可以去看其他学习资料。

1
class Solution {
2
    public boolean repeatedSubstringPattern(String s) {
3
        return kmp(s+s, s);
4
    }
5
6
    public boolean kmp(String query, String pattern){
7
        int n = query.length();
8
        int m = pattern.length();
9
        int[] fail = new int[m];
10
        Arrays.fill(fail, -1);
11
        for(int i=1; i<m; i++){
12
            int j = fail[i-1];
13
            while(j!=-1 && pattern.charAt(i)!=pattern.charAt(j+1)){
14
                j = fail[j];
15
            }
16
            if(pattern.charAt(i) == pattern.charAt(j+1)){
17
                fail[i] = j+1;
18
            }
19
        }
20
        int match = -1;
21
        for(int i=1; i<n-1; i++){
22
            while(match!=-1 && pattern.charAt(match+1)!=query.charAt(i)){
23
                match = fail[match];
24
            }
25
            if(pattern.charAt(match+1) == query.charAt(i)){
26
                match++;
27
                if(match == m-1){
28
                    return true;
29
                }
30
            }
31
        }
32
        return false;
33
    }
34
}

复杂度分析：

  • 时间复杂度：$O(n)$。
  • 空间复杂度：$O(n)$。

KMP算法模板

1
public class KMP {
2
    public boolean kmp(String query, String pattern) {
3
        int n = query.length();
4
        int m = pattern.length();
5
        int[] fail = new int[m];
6
        Arrays.fill(fail, -1);
7
        // 填充fail数组，求公共前后缀长度
8
        for (int i = 1; i < m; ++i) {
9
            int j = fail[i - 1];
10
            while (j != -1 && pattern.charAt(j + 1) != pattern.charAt(i)) {
11
                j = fail[j];
12
            }
13
            if (pattern.charAt(j + 1) == pattern.charAt(i)) {
14
                fail[i] = j + 1;
15
            }
16
        }
17
        // 开始匹配
18
        int match = -1;
19
        for (int i = 0; i < n; ++i) {
20
            while (match != -1 && pattern.charAt(match + 1) != query.charAt(i)) {
21
                match = fail[match];
22
            }
23
            if (pattern.charAt(match + 1) == query.charAt(i)) {
24
                ++match;
25
                // 匹配成功
26
                if (match == m - 1) {
27
                    return true;
28
                }
29
            }
30
        }
31
        return false;
32
    }
33
}

注意在这题中开始匹配的时候应该从ss第二个字符开始匹配直到倒数第二个字符结束，这一点与一般的kmp算法有区别。