N皇后


回溯
经典的回溯问题。在每一行枚举皇后的位置,然后进行判断是否合法,即任意两个皇后不能在同一行,同一列或者同一斜线,如果合法,就进入下一行继续枚举,否则回溯。
1 | class Solution { |
2 | List<List<String>> ans = new ArrayList<List<String>>(); |
3 | int N; |
4 | char[][] board; |
5 | public List<List<String>> solveNQueens(int n) { |
6 | N = n; |
7 | board = new char[n][n]; |
8 | for(int i=0; i<n; i++){ |
9 | Arrays.fill(board[i], '.'); |
10 | } |
11 | dfs(0); |
12 | return ans; |
13 | } |
14 | |
15 | public void dfs(int curRow){ |
16 | if(curRow == N){ |
17 | List<String> temp = new ArrayList<String>(); |
18 | for(char[] cur : board){ |
19 | temp.add(String.valueOf(cur)); |
20 | } |
21 | ans.add(temp); |
22 | return; |
23 | } |
24 | for(int i=0; i<N; i++){ |
25 | int x = curRow; |
26 | int y = i; |
27 | if(isValid(x, y)){ |
28 | board[x][y] = 'Q'; |
29 | dfs(curRow+1); |
30 | board[x][y] = '.'; |
31 | } |
32 | } |
33 | } |
34 | |
35 | public boolean isValid(int x, int y){ |
36 | // 检查行 |
37 | for(int i=0; i<y; i++){ |
38 | if(board[x][i] == 'Q'){ |
39 | return false; |
40 | } |
41 | } |
42 | // 检查列 |
43 | for(int i=0; i<x; i++){ |
44 | if(board[i][y] == 'Q'){ |
45 | return false; |
46 | } |
47 | } |
48 | // 检查对角线 |
49 | for(int i=x-1, j=y-1; i>=0 && j>=0; i--, j--){ |
50 | if(board[i][j] == 'Q'){ |
51 | return false; |
52 | } |
53 | } |
54 | for(int i=x-1, j=y+1; i>=0 && j<N; i--, j++){ |
55 | if(board[i][j] == 'Q'){ |
56 | return false; |
57 | } |
58 | } |
59 | return true; |
60 | } |
61 | } |
复杂度分析:
- 时间复杂度:$O(n!)$,第一行枚举$n$个位置,第二行枚举$n-1$个位置,以此类推。
- 空间复杂度:$O(n^2)$,棋盘初始化使用二维数组初始化。
我们可以对空间复杂度进行优化。可以发现对于同一主对角线(左上到右下)的点来说,他们的横坐标减去纵坐标是一个定值。对于同一副对角线(右上到坐下)的点来说,他们的横坐标加纵坐标是一个定值。那么我们可以使用集合来存储。
1 | class Solution { |
2 | List<List<String>> ans; |
3 | int N; |
4 | Set<Integer> columns;// 存储不同的列 |
5 | Set<Integer> diagonals1;// 存储不同的主对角线 |
6 | Set<Integer> diagonals2;// 存储不同的副对角线 |
7 | int[] queens; |
8 | public List<List<String>> solveNQueens(int n) { |
9 | N = n; |
10 | ans = new ArrayList<List<String>>(); |
11 | columns = new HashSet<Integer>(); |
12 | diagonals1 = new HashSet<Integer>(); |
13 | diagonals2 = new HashSet<Integer>(); |
14 | queens = new int[n]; |
15 | Arrays.fill(queens, -1); |
16 | backtrack(0); |
17 | return ans; |
18 | } |
19 | |
20 | public void backtrack(int row){ |
21 | if(row == N){ |
22 | List<String> temp = generateAns(); |
23 | ans.add(temp); |
24 | return; |
25 | } |
26 | for(int i=0; i<N; i++){ |
27 | // 同一列有皇后 |
28 | if(columns.contains(i)){ |
29 | continue; |
30 | } |
31 | // 同一主对角线有皇后 |
32 | if(diagonals1.contains(row-i)){ |
33 | continue; |
34 | } |
35 | // 同一副对角线有皇后 |
36 | if(diagonals2.contains(row+i)){ |
37 | continue; |
38 | } |
39 | columns.add(i); |
40 | diagonals1.add(row-i); |
41 | diagonals2.add(row+i); |
42 | queens[row] = i; |
43 | backtrack(row+1); |
44 | // 回溯 |
45 | queens[row] = -1; |
46 | columns.remove(i); |
47 | diagonals1.remove(row-i); |
48 | diagonals2.remove(row+i); |
49 | } |
50 | } |
51 | |
52 | public List<String> generateAns(){ |
53 | List<String> solution = new ArrayList<String>(); |
54 | for(int i=0; i<N; i++){ |
55 | char[] temp = new char[N]; |
56 | Arrays.fill(temp, '.'); |
57 | temp[queens[i]] = 'Q'; |
58 | solution.add(new String(temp)); |
59 | } |
60 | return solution; |
61 | } |
62 | } |
我们使用了$O(n)$的空间复杂度来存储皇后的信息。我们可以使用位运算继续优化空间复杂度到$O(1)$来存储皇后的信息。
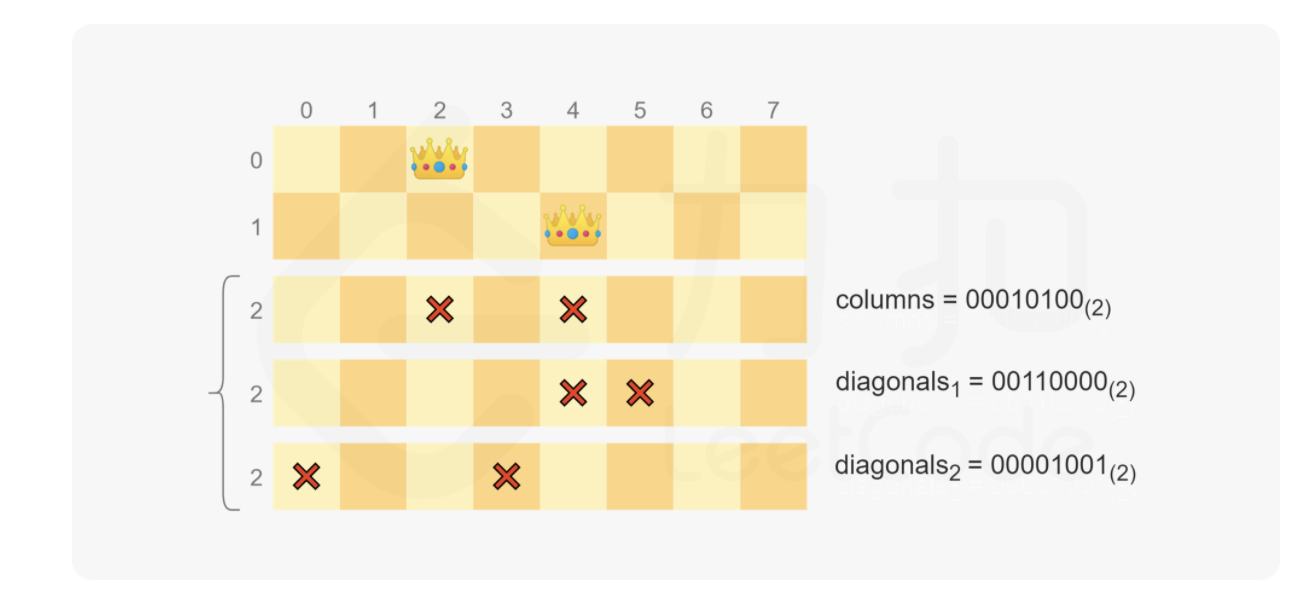
每次放置皇后时,三个整数的按位或运算的结果即为不能放置皇后的位置,其余位置即为可以放置皇后的位置。可以通过$ (2^n-1)&(\sim(\textit{columns} | \textit{diagonals}_1 | \textit{diagonals}_2))$得到可以放置皇后的位置(该结果的值为 $1$ 的位置表示可以放置皇后的位置),然后遍历这些位置,尝试放置皇后并得到可能的解。
遍历可以放置皇后的位置时,可以利用以下两个按位与运算的性质:
$x
&(-x)$ 可以获得 $x$ 的二进制表示中的最低位的$1$的位置,其结果是只剩最低位的$1$,其余为$,0$,例如$3 & (-3)=1$;$x
&(x-1)$ 可以将 $x$ 的二进制表示中的最低位的 $1$ 置成 $0$。
具体做法是,每次获得可以放置皇后的位置中的最低位,并将该位的值置成 $0$,尝试在该位置放置皇后。这样即可遍历每个可以放置皇后的位置。
1 | class Solution { |
2 | List<List<String>> ans; |
3 | int N; |
4 | int[] queens; |
5 | public List<List<String>> solveNQueens(int n) { |
6 | N = n; |
7 | ans = new ArrayList<List<String>>(); |
8 | queens = new int[n]; |
9 | Arrays.fill(queens, -1); |
10 | backtrack(0, 0, 0, 0); |
11 | return ans; |
12 | } |
13 | |
14 | public void backtrack(int row, int columns, int diagonals1, int diagonals2){ |
15 | if(row == N){ |
16 | List<String> temp = generateAns(); |
17 | ans.add(temp); |
18 | return; |
19 | } |
20 | int availablePositions = ((1<<N)-1) & (~(columns|diagonals1|diagonals2)); |
21 | while(availablePositions != 0){ |
22 | int position = availablePositions & (-availablePositions); |
23 | availablePositions = availablePositions & (availablePositions-1); |
24 | queens[row] = Integer.bitCount(position-1); // 计算最低位的1的位置 |
25 | backtrack(row+1, columns|position, (diagonals1 | position)<<1, (diagonals2 | position)>>1); |
26 | queens[row] = -1; |
27 | } |
28 | } |
29 | |
30 | public List<String> generateAns(){ |
31 | List<String> solution = new ArrayList<String>(); |
32 | for(int i=0; i<N; i++){ |
33 | char[] temp = new char[N]; |
34 | Arrays.fill(temp, '.'); |
35 | temp[queens[i]] = 'Q'; |
36 | solution.add(new String(temp)); |
37 | } |
38 | return solution; |
39 | } |
40 | } |