207场周赛
##1.重新排列单词间的空格

模拟题,细心即可。
1 | class Solution { |
2 | public String reorderSpaces(String text) { |
3 | char[] str = text.toCharArray(); |
4 | int spacenum = 0; |
5 | int wordnum = 0; |
6 | List<String> wordlist = new ArrayList<String>(); |
7 | for(int i=0; i<str.length; i++){ |
8 | if(str[i] == ' '){ |
9 | spacenum++; |
10 | }else{ |
11 | int j=i; |
12 | while(i<str.length){ |
13 | |
14 | if(str[i]>='a' && str[i]<='z'){ |
15 | i++; |
16 | }else { |
17 | spacenum++; |
18 | break; |
19 | } |
20 | } |
21 | String word = text.substring(j, i); |
22 | wordlist.add(word); |
23 | } |
24 | } |
25 | |
26 | wordnum = wordlist.size(); |
27 | if(wordnum - 1==0){ |
28 | StringBuilder sb = new StringBuilder(); |
29 | char[] space = new char[spacenum]; |
30 | Arrays.fill(space, ' '); |
31 | sb.append(wordlist.get(0)); |
32 | sb.append(space); |
33 | return sb.toString(); |
34 | } |
35 | int a = spacenum / (wordnum-1); |
36 | int b = spacenum % (wordnum-1); |
37 | char[] aa = new char[a]; |
38 | char[] bb = new char[b]; |
39 | Arrays.fill(aa, ' '); |
40 | Arrays.fill(bb, ' '); |
41 | StringBuilder sb = new StringBuilder(); |
42 | for(int i=0; i<wordlist.size(); i++){ |
43 | String word = wordlist.get(i); |
44 | if(i == wordlist.size()-1){ |
45 | sb.append(word); |
46 | }else { |
47 | sb.append(word); |
48 | sb.append(aa); |
49 | } |
50 | } |
51 | |
52 | sb.append(bb); |
53 | return sb.toString(); |
54 | } |
55 | } |
复杂度分析:
- 时间复杂度:$O(N)$。
- 空间复杂度:$O(N)$。
2.拆分字符串使唯一子字符串的数目最大
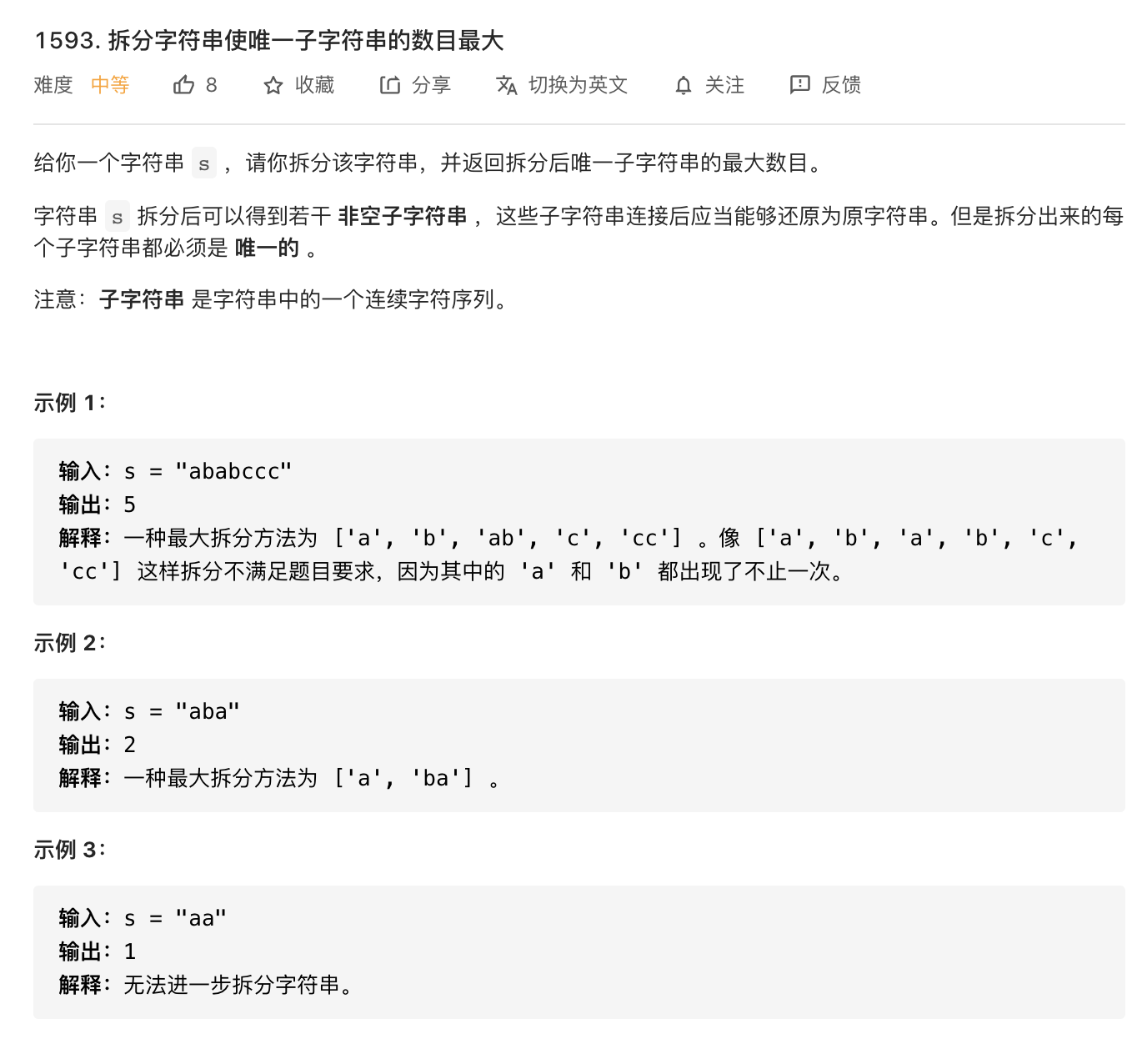
用一个集合存储每个出现过的子字符串。对于每个位置上的字符串,都有拆分和不拆分两种选择,可以选择拆分,如果不满足条件(拆分出的子字符串未出现过)就回溯。
1 | class Solution { |
2 | int max = 0; |
3 | Set<String> set = new HashSet<String>(); |
4 | public int maxUniqueSplit(String s) { |
5 | dfs(0,0,1,s); |
6 | return max; |
7 | } |
8 | |
9 | public void dfs(int start, int end, int res, String s){ |
10 | if(end == s.length()-1){ |
11 | if(set.contains(s.substring(start,end+1))){ |
12 | return; |
13 | }else { |
14 | max = Math.max(max, res); |
15 | return; |
16 | } |
17 | } |
18 | String cur = s.substring(start, end+1); |
19 | if(!set.contains(cur)){ |
20 | set.add(cur); |
21 | dfs(end+1, end+1, res+1, s); |
22 | set.remove(cur); |
23 | } |
24 | dfs(start, end+1, res, s); |
25 | } |
26 | } |
复杂度分析:
- 时间复杂度:$O(N)$。
- 空间复杂度:$O(N)$。
3.矩阵的最大非负积

因为最大的结果可能由一个正数乘以一个正数得到,也可能由一个负数乘以一个负数得到,因此需要分别记录最大值和最小值。当前位置[x,y]的最大值和最小值由[x-1,y]和[x,y-1]与当前位置的值grid[x][y]得到,由此可以得到状态转移方程。
1 | class Solution { |
2 | public int maxProductPath(int[][] grid) { |
3 | int m = grid.length; |
4 | int n = grid[0].length; |
5 | long[][] pos = new long[m][n]; |
6 | long[][] neg = new long[m][n]; |
7 | long mod = (long)(1e9+7); |
8 | pos[0][0] = neg[0][0] = grid[0][0]; |
9 | for(int i=1; i<m; i++){ |
10 | pos[i][0] = pos[i-1][0]*grid[i][0]; |
11 | neg[i][0] = neg[i-1][0]*grid[i][0]; |
12 | } |
13 | for(int j=1; j<n; j++){ |
14 | pos[0][j] = pos[0][j-1]*grid[0][j]; |
15 | neg[0][j] = neg[0][j-1]*grid[0][j]; |
16 | } |
17 | for(int i=1; i<m; i++){ |
18 | for(int j=1; j<n; j++){ |
19 | long a = pos[i-1][j] * grid[i][j]; |
20 | long b = neg[i-1][j] * grid[i][j]; |
21 | long c = pos[i][j-1] * grid[i][j]; |
22 | long d = neg[i][j-1] * grid[i][j]; |
23 | pos[i][j] = Math.max(Math.max(a,b), Math.max(c,d)); |
24 | neg[i][j] = Math.min(Math.min(a,b), Math.min(c,d)); |
25 | } |
26 | } |
27 | int res = (int) Math.max(pos[m-1][n-1]%mod, neg[m-1][n-1]%mod); |
28 | return (res<0)? -1:res; |
29 | } |
30 | } |
复杂度分析:
- 时间复杂度:$O(N*M)$。
- 空间复杂度:$O(N*M)$。
4.连通两组点的最小成本

问题等价于: 在一个矩阵中选取一些值, 满足矩阵的每一行和每一列都至少有一个元素被选中, 同时选中元素的总和最小 (此矩阵就是 cost 矩阵)。
由于矩阵的列数较少, 我们可以用状压 DP 来表示每一行的选取情况, 假设矩阵有 m 行 n 列, 那么我们维护一个 DP 矩阵 dp[m][1 << n],dp[i][j]表示当前选取到第 $i$ 行, 每列的选取状况为 $j$ 时总的最小开销, 其中 $j$ 的第 $k$ 位为 $1$ 即表示第 $k$ 列已经被选取过了. 那么状态转移方程为
$dp[i][j|k] = Math.min(dp[i][j|k], dp[i - 1][k] + costMatrix[i][j])$
其中 $costMatrix[i][j] $表示第 $i$ 行选取状况为 $j$ 时该行被选取得元素总和。
1 | class Solution { |
2 | public int connectTwoGroups(List<List<Integer>> cost) { |
3 | int m = cost.size(), n = cost.get(0).size(); |
4 | int[][] costMatrix = new int[m][1 << n]; |
5 | for (int k = 0; k < m; k++) { |
6 | for (int i = 0; i < (1 << n); i++) { |
7 | int sum = 0; |
8 | for (int j = 0; j < n; j++) { |
9 | if ((i & (1 << j)) > 0) |
10 | sum += cost.get(k).get(j); |
11 | } |
12 | costMatrix[k][i] = sum; |
13 | } |
14 | } |
15 | int[][] dp = new int[m][1 << n]; |
16 | for (int i = 1; i < m; i++) |
17 | Arrays.fill(dp[i], Integer.MAX_VALUE); |
18 | dp[0] = costMatrix[0]; |
19 | for (int i = 1; i < m; i++) |
20 | for (int j = 1; j < (1 << n); j++) |
21 | for (int k = 1; k < (1 << n); k++) |
22 | dp[i][j | k] = Math.min(dp[i][j | k], dp[i - 1][k] + costMatrix[i][j]); |
23 | return dp[m - 1][(1 << n) - 1]; |
24 | } |
25 | } |
复杂度分析:
- 时间复杂度:$O(M2^N2^N)$。
- 空间复杂度:$O(N*M)$。