0%

leetcode每日一题-从中序与后序遍历序列构造二叉树

Posted on In ,

从中序与后序遍历序列构造二叉树

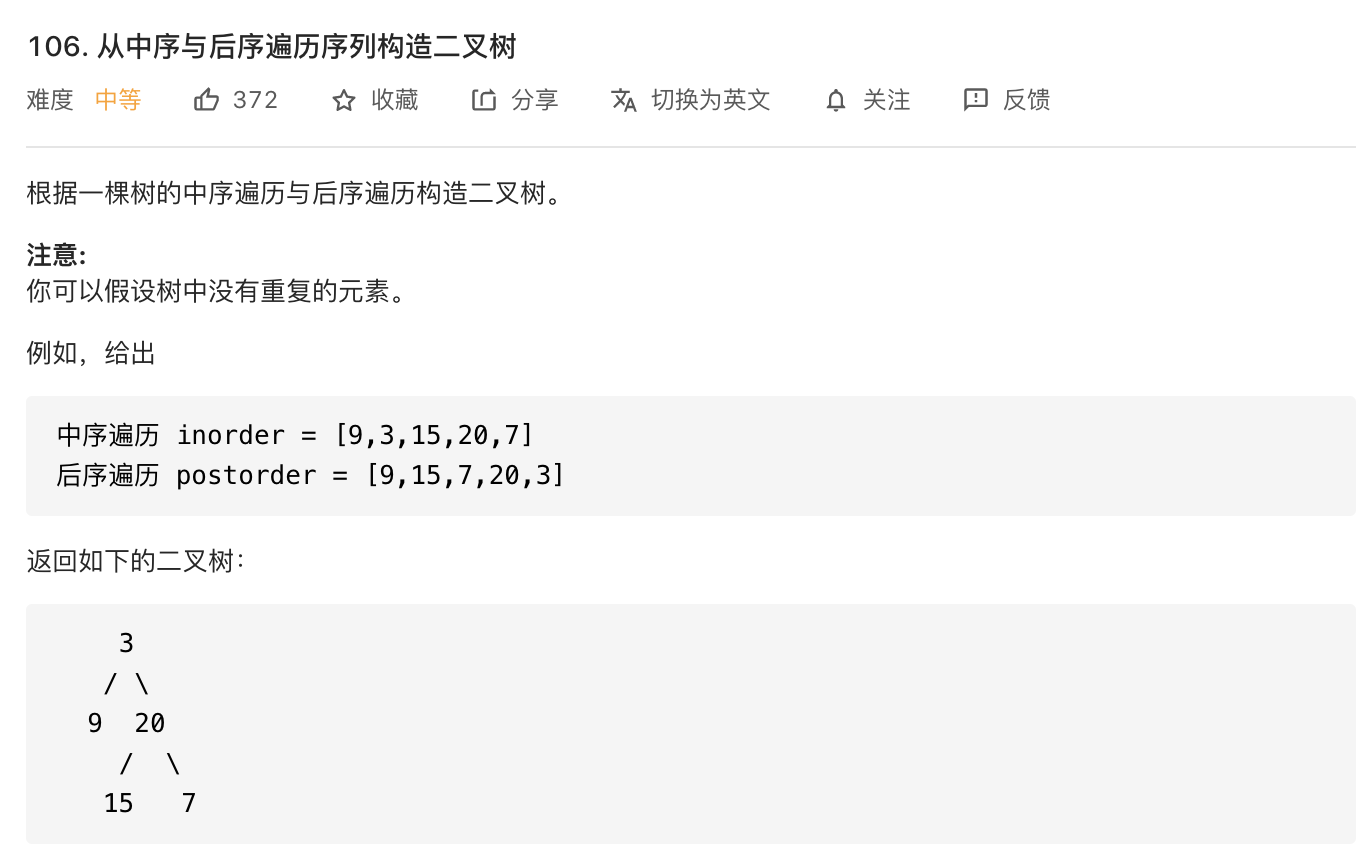
image1

首先需要明白的是中序遍历的顺序是：(左子树)(根)(右子树)。而后序遍历的顺序是(左子树)(右子树)(根)。由于没有重复元素，那么我们可以每次从后序序列最后一个值确定根节点的值root.val，然后根据root.val 在中序序列中查找根节点的位置index，由此可以确定左右子树的大小，左子树的范围就是[inorder_begin,index-1]，大小为leftsub = index-inorder_begin，右子树的范围是[index+1,inorder_end]，大小为rightsub = inorder_end-index。知道了左右子树的大小，那么就可以确定在后序序列中左右子树的范围，左子树的范围为[posorder_begin,posorder_begin+leftsub-1]，右子树的范围为[posorder_end-rightsub,posorder_end-1]。之后就可以递归地构造子树即可。为了在中序序列中查找方便，可以使用哈希表记录每个数在中序序列中的位置。

1
/**
2
 * Definition for a binary tree node.
3
 * public class TreeNode {
4
 *     int val;
5
 *     TreeNode left;
6
 *     TreeNode right;
7
 *     TreeNode(int x) { val = x; }
8
 * }
9
 */
10
class Solution {
11
    int n;
12
    Map<Integer, Integer> map = new HashMap<>();
13
    int[] postorder;
14
    int[] inorder;
15
    public TreeNode buildTree(int[] inorder, int[] postorder) {
16
        this.inorder = inorder;
17
        this.postorder = postorder;
18
        n = inorder.length;
19
        for(int i=0; i<n; i++){
20
            map.put(inorder[i], i);
21
        }
22
        TreeNode root = solve(0, n-1, 0, n-1);
23
        return root;
24
    }
25
26
    public TreeNode solve(int inbegin, int inend, int posbegin, int posend){
27
        if(inbegin>inend || posbegin>posend){
28
            return null;
29
        }
30
        int val = postorder[posend];
31
        TreeNode root = new TreeNode(val);
32
        int index = map.get(val);
33
        int leftsub_size = index-inbegin;
34
        int rightsub_size = inend-index;
35
        root.left = solve(inbegin, index-1, posbegin, posbegin+leftsub_size-1);
36
        root.right = solve(index+1, inend, posend-rightsub_size, posend-1);
37
        
38
        return root;
39
    }
40
}

从前序与中序遍历序列构造二叉树

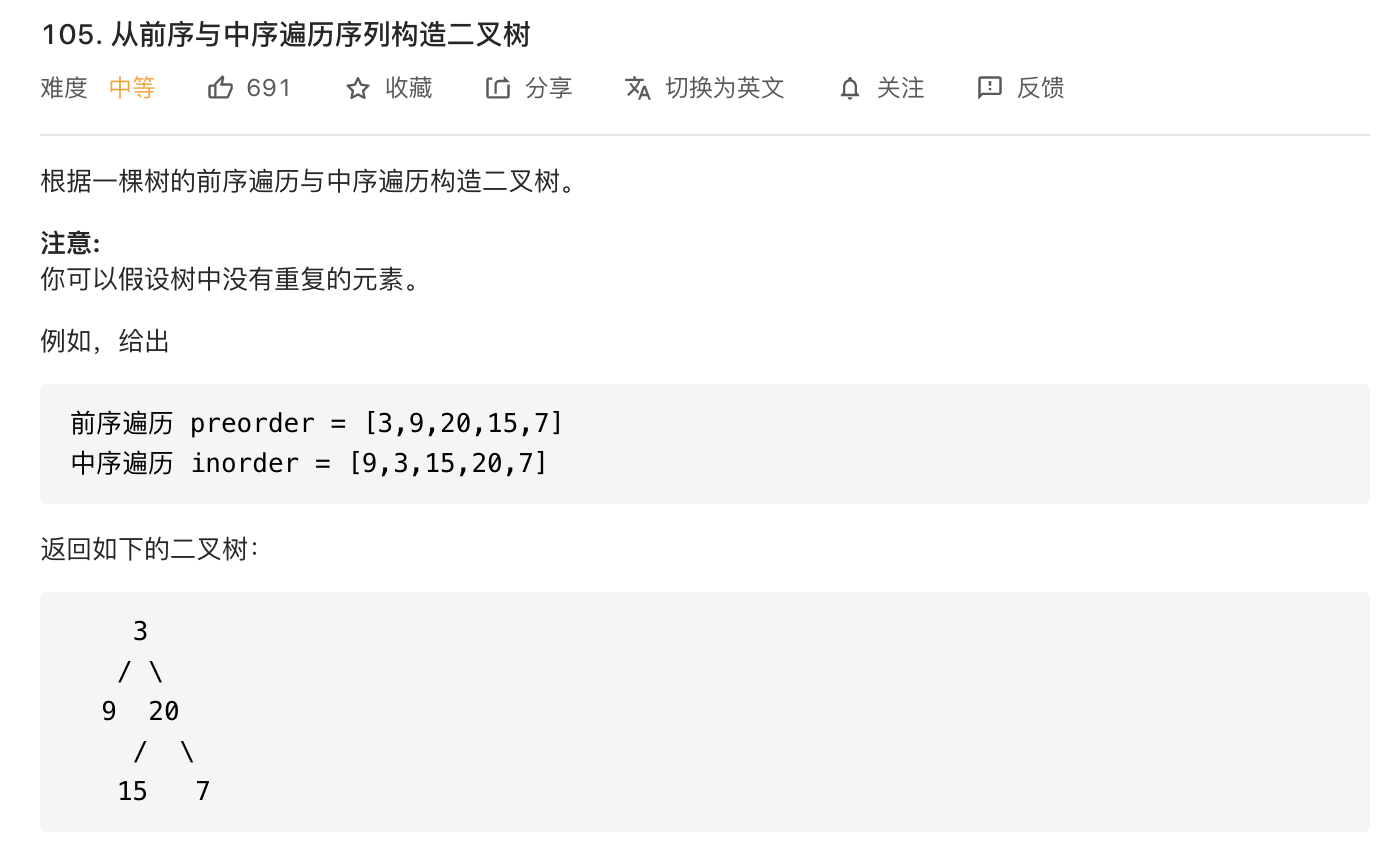
image2

同样的，需要明白的是中序遍历的顺序是：(左子树)(根)(右子树)。而前序遍历的顺序是(根)(左子树)(右子树)。由于没有重复元素，那么我们可以每次从前序序列第一个值确定根节点的值root.val，然后根据root.val 在中序序列中查找根节点的位置index，由此可以确定左右子树的大小，左子树的范围就是[inorder_begin,index-1]，大小为leftsub = index-inorder_begin，右子树的范围是[index+1,inorder_end]，大小为rightsub = inorder_end-index。知道了左右子树的大小，那么就可以确定在前序序列中左右子树的范围，左子树的范围为[preorder_begin+1,preorder_begin+1+leftsub-1]，右子树的范围为[posorder_end-rightsub+1,posorder_end]。之后就可以递归地构造子树即可。为了在中序序列中查找方便，可以使用哈希表记录每个数在中序序列中的位置。

1
class Solution {
2
    Map<Integer, Integer> map;
3
    int[] preorder;
4
    int[] inorder;
5
    public TreeNode buildTree(int[] preorder, int[] inorder) {
6
        this.preorder = preorder;
7
        this.inorder = inorder;
8
        int n = preorder.length;
9
        map = new HashMap<>();
10
        for(int i=0;i<n;i++){
11
            map.put(inorder[i],i);
12
        }
13
        TreeNode root = solve(0, n-1, 0, n-1);
14
        return root;
15
    }
16
17
    public TreeNode solve(int prebegin, int preend, int inbegin, int inend){
18
        if(prebegin>preend || inbegin>inend){
19
            return null;
20
        }
21
        int val = preorder[prebegin];
22
        TreeNode root = new TreeNode(val);
23
        int index = map.get(val);
24
        int leftsub_size = index-inbegin;
25
        int rightsub_size = inend-index;
26
        root.left = solve(prebegin+1, prebegin+1+leftsub_size-1,inbegin,index-1);
27
        root.right = solve(preend-rightsub_size+1, preend, index+1, inend);
28
        return root;
29
    }
30
}

#从前序与后序遍历序列构造二叉树

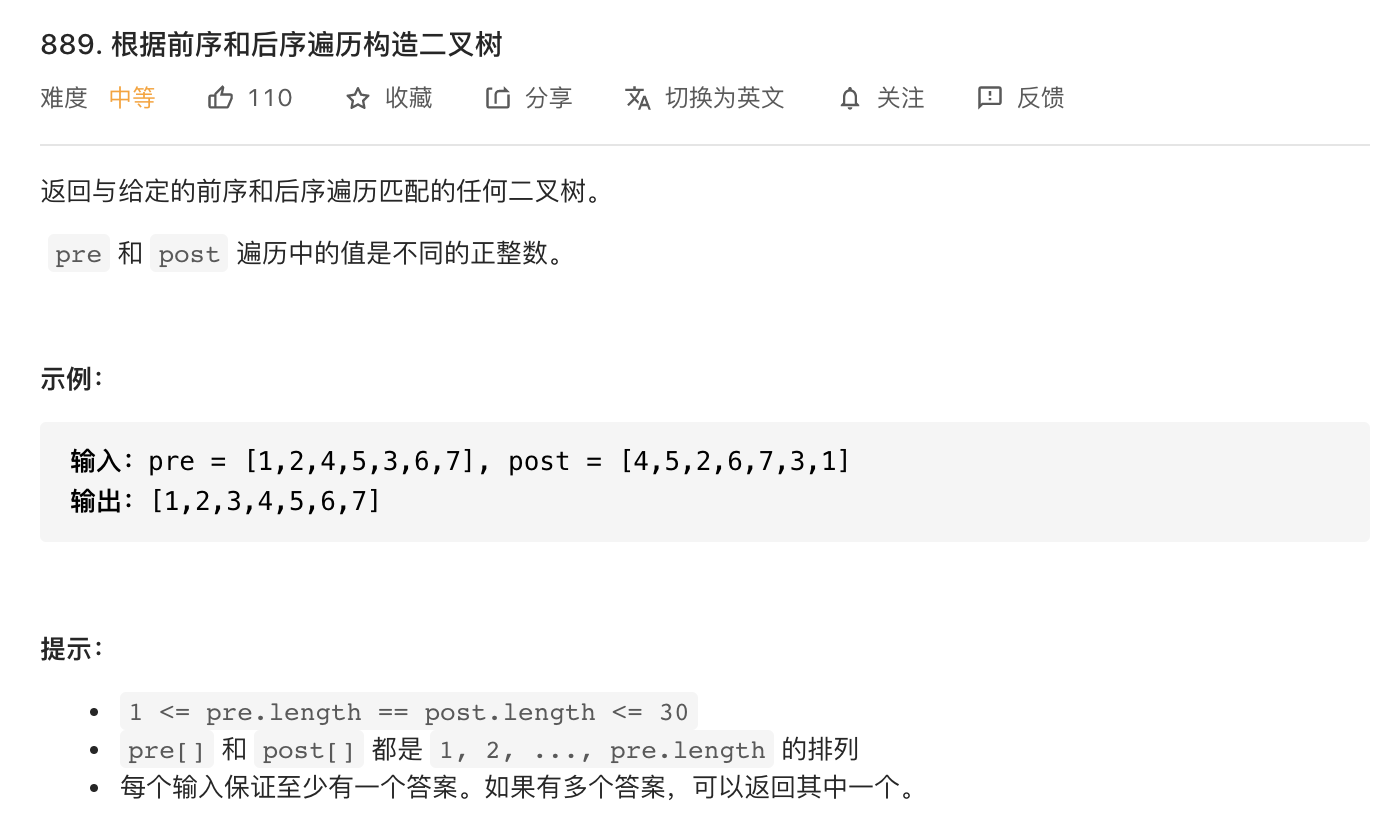
image3

思路和前两题一样，前序遍历的顺序是(根)(左子树)(右子树)。而后序遍历的顺序是(左子树)(右子树)(根)。我们可以知道前序序列中第一个是根节点的值，第二个值就是左子树中根节点的值leftroot.val，而在后序序列中，左子树的根节点是在左子树序列的最后一个节点，那么通过在后序序列中查找leftroot.val就能确定左子树的根节点的位置index。由此可以确定在后序序列中左子树的范围为[posorder_begin,index]，左子树的大小为leftsub = index-posorder_begin+1，右子树的范围为[index+1,posorder_end-1]，右子树大小为rightsub = posorder_end-1-(index+1)+1 = posorder_end-1-index。之后就可以递归的构造左右子树了。在前序序列中左子树的范围为[preorder_begin+1,preorder_begin+1+leftsub-1]，右子树的范围为[preorder_end-rightsub+1, preorder_end]。

1
class Solution {
2
    int[] pre;
3
    int[] post;
4
    Map<Integer, Integer> map = new HashMap<>();
5
    public TreeNode constructFromPrePost(int[] pre, int[] post) {
6
        this.pre = pre;
7
        this.post = post;
8
        int n = pre.length;
9
        for(int i=0; i<n; i++){
10
            map.put(post[i], i);
11
        }
12
        TreeNode root = solve(0, n-1, 0, n-1);
13
        return root;
14
    }
15
16
    public TreeNode solve(int prebegin, int preend, int posbegin, int posend){
17
        if(prebegin>preend || posbegin>posend){
18
            return null;
19
        }
20
        int val = pre[prebegin];
21
        TreeNode root = new TreeNode(val);
22
        if(prebegin == preend){
23
            return root;
24
        }
25
        int index = map.get(pre[prebegin+1]);
26
        int leftsub_size = index-posbegin+1;
27
        int rightsub_size = posend-1-index;
28
        root.left = solve(prebegin+1, prebegin+1+leftsub_size-1,posbegin, index);
29
        root.right = solve(preend-rightsub_size+1, preend, index+1, posend-1);
30
        return root;
31
    }
32
}