0%

leetcode每日一题-填充每个节点的下一个右侧节点指针II

Posted on In ,

填充每个节点的下一个右侧节点指针II

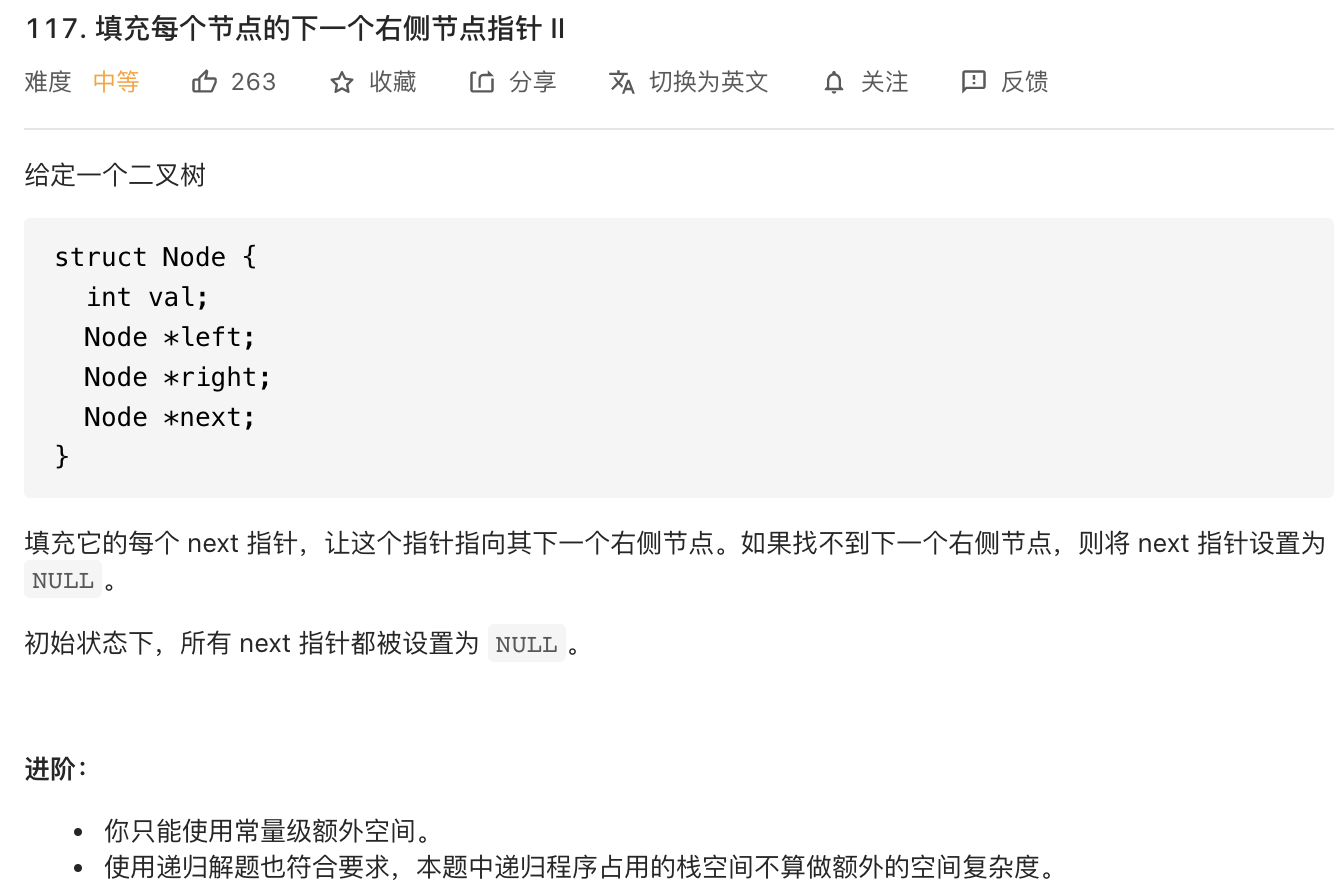
image1

image1

方法一：层序遍历

这道题希望我们把二叉树各个层的点组织成链表，一个非常直观的思路是层次遍历。树的层次遍历基于广度优先搜索，它按照层的顺序遍历二叉树，在遍历第 $i$层前，一定会遍历完第 $i−1$ 层。

我们可以在遍历每一层的时候修改这一层节点的 \rm nextnext 指针，这样就可以把每一层都组织成链表。

1
/*
2
// Definition for a Node.
3
class Node {
4
    public int val;
5
    public Node left;
6
    public Node right;
7
    public Node next;
8
9
    public Node() {}
10
    
11
    public Node(int _val) {
12
        val = _val;
13
    }
14
15
    public Node(int _val, Node _left, Node _right, Node _next) {
16
        val = _val;
17
        left = _left;
18
        right = _right;
19
        next = _next;
20
    }
21
};
22
*/
23
24
class Solution {
25
    public Node connect(Node root) {
26
        Queue<Node> queue = new LinkedList<Node>();
27
        if(root == null){
28
            return root;
29
        }
30
        //root.next = null;
31
        queue.offer(root);
32
        while(!queue.isEmpty()){
33
            int size = queue.size();
34
            Node last = null;
35
            for(int i=0; i<size; i++){
36
                Node cur = queue.poll();
37
                if(cur!=null && cur.left!=null){
38
                    queue.offer(cur.left);
39
                }
40
                if(cur!=null && cur.right!=null){
41
                    queue.offer(cur.right);
42
                }
43
                if(i != 0){
44
                    last.next = cur;
45
                }
46
                last = cur;
47
            }
48
        }
49
        return root;
50
    }
51
}

复杂度分析：

  • 时间复杂度：$O(N)$。
  • 空间复杂度：$O(N)$。

方法二：使用已建立的next指针

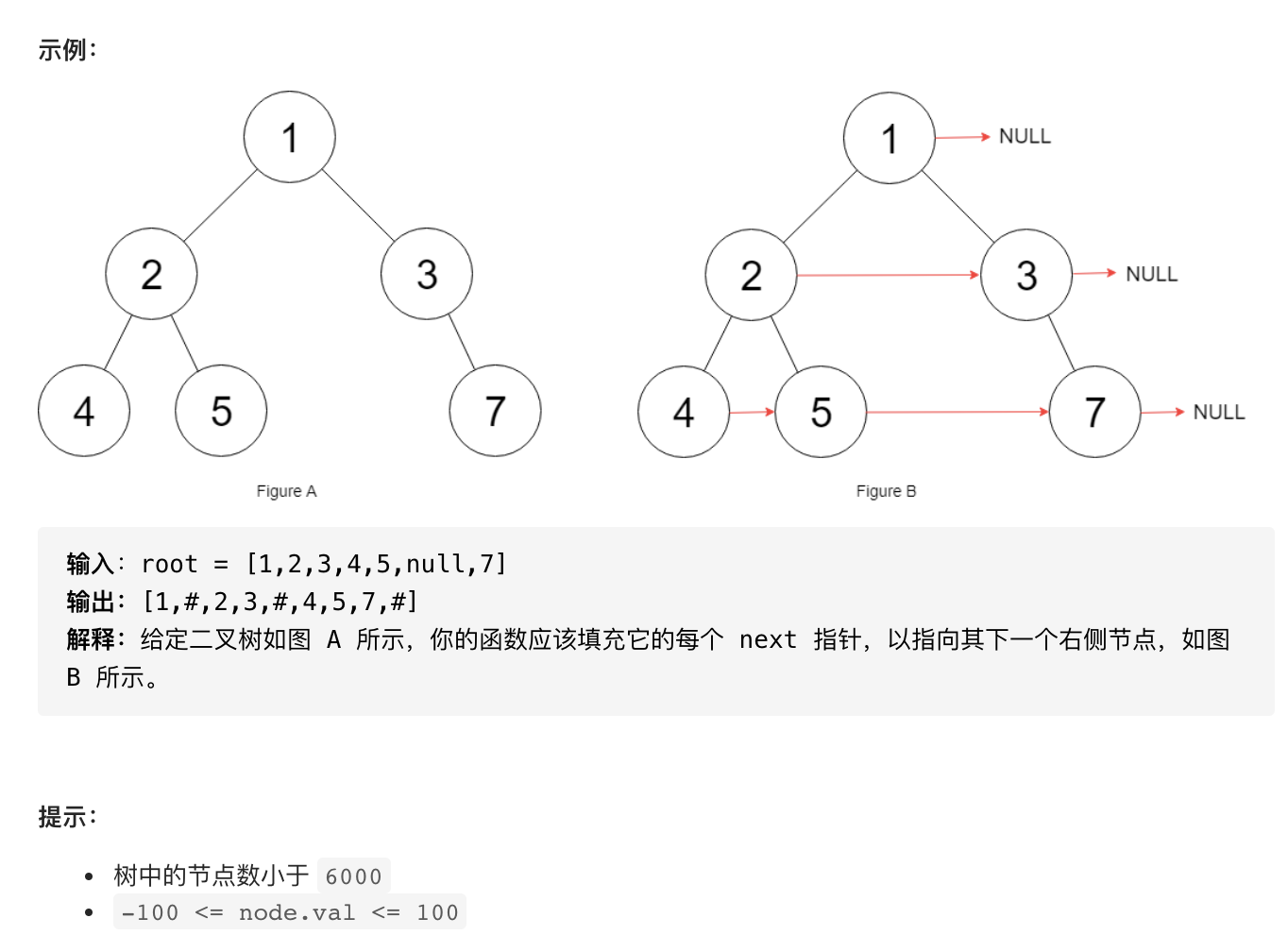
我们可以根据上一层建立的next指针来建立下一层的指针。以上图中的二叉树为例，假设第二层的next指针已经建立好，我们需要为第三层建立next指针。我们在遍历第二层链表的同时顺便将第三层next指针建好。首先访问节点2，它的左子孩子是节点4，那么节点4就是第三层链表的头部，同时节点2也有右子孩子节点5，此时将节点4的next指针指向节点5。之后再根据节点2的next指针访问节点5，节点5没有左子孩子，但是有右子孩子，那么就可以将节点5也就是节点2的右子孩子的next指针指向节点5的右子孩子节点7。此时第三层的next指针就建立完毕，如果还有第四层，就可以根据第三层的next指针建立第四层链表。我们需要两个节点分别记录当前层遍历到的节点以及下一层要建立next指针的节点。

1
/*
2
// Definition for a Node.
3
class Node {
4
    public int val;
5
    public Node left;
6
    public Node right;
7
    public Node next;
8
9
    public Node() {}
10
    
11
    public Node(int _val) {
12
        val = _val;
13
    }
14
15
    public Node(int _val, Node _left, Node _right, Node _next) {
16
        val = _val;
17
        left = _left;
18
        right = _right;
19
        next = _next;
20
    }
21
};
22
*/
23
24
class Solution {
25
    public Node connect(Node root) {
26
        if(root == null){
27
            return root;
28
        }
29
      	// 哑指针，next指针指向链表头
30
        Node dummy = new Node(0);
31
      	// cur指向当前层遍历到的节点
32
        Node cur = root;
33
        while(cur != null){
34
          	// 初始化哑指针
35
            dummy.next = null;
36
            Node pre = dummy;
37
          	// 遍历当前层
38
            while(cur != null){
39
              	// pre指向下一层要建立next指针的节点
40
                if(cur.left != null){
41
                    pre.next = cur.left;
42
                    pre = pre.next;
43
                }
44
                if(cur.right != null){
45
                    pre.next = cur.right;
46
                    pre = pre.next;
47
                }
48
                cur = cur.next;
49
            }
50
          	// 当前层已经遍历完，去下一层
51
          	// 哑指针的next指针指向下一层的头
52
            cur = dummy.next;
53
        }
54
        return root;
55
    }
56
}

复杂度分析：

  • 时间复杂度：$O(N)$。
  • 空间复杂度：$O(1)$。