0%

leetcode每日一题-环形链表

Posted on In ,

环形链表

image1

可以使用两个指针，快指针每次走2步，慢指针每次走1步，如果链表有环，那么两个指针一定可以在链表中的某个节点相遇。

1
/**
2
 * Definition for singly-linked list.
3
 * class ListNode {
4
 *     int val;
5
 *     ListNode next;
6
 *     ListNode(int x) {
7
 *         val = x;
8
 *         next = null;
9
 *     }
10
 * }
11
 */
12
public class Solution {
13
    public boolean hasCycle(ListNode head) {
14
        if(head==null || head.next==null){
15
            return false;
16
        }
17
        ListNode fast = head, slow = head;
18
        while(fast != null){
19
            if(fast.next != null){
20
                fast = fast.next.next;
21
            }else{
22
              	// fast到达链表末尾
23
                return false;
24
            }
25
            slow = slow.next;
26
            if(fast == slow){
27
                return true;
28
            }
29
        }
30
        return false;
31
    }
32
}

复杂度分析：

  • 时间复杂度：$O(N)$。
  • 空间复杂度：$O(1)$。

image2

我们依然可以使用两个指针$fast$和$slow$。$fast$每次前进两步，$slow$每次前进一步，如果链表中有环，那么两个指针就会相遇，考虑此时相遇的情况如下图。

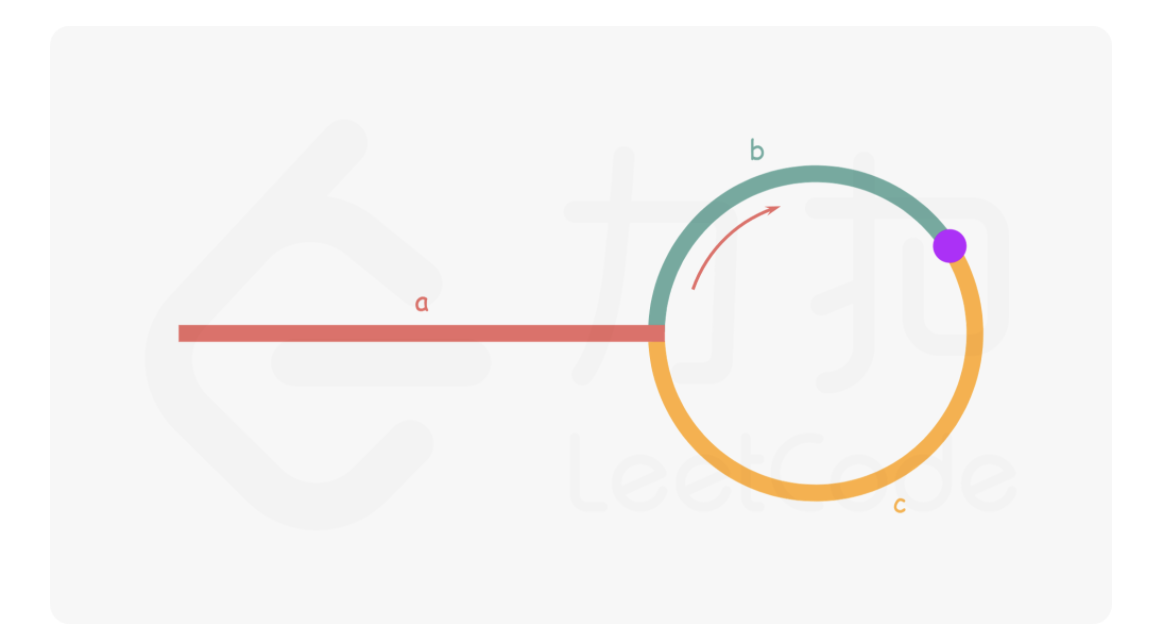
image3

设此时链表头到环入口的距离为$a$，$slow$指针进入环后又走了距离$b$与$fast$指针相遇，假设此时$fast$指针已经走了$n$圈，那么$fast$指针走的总距离为$a+n(b+c)+b=a+(n+1)b+nc$。$slow$指针走的距离为$a+b$。由题可知，$fast$走的距离是$slow$走的距离的两倍，那么就能得到$a+(n+1)b+nc=2(a+b)=>a = c+(n-1)(b+c)$。根据$a$和$c$的等价关系可以发现从相遇点到入环点的距离再加上$n-1$圈长就等于从链表头到入环点的距离。此时再设一个指针$ptr$从链表头出发，每次前进一步，继续移动$slow$指针，那么两个指针就会在入环口相遇。

1
/**
2
 * Definition for singly-linked list.
3
 * class ListNode {
4
 *     int val;
5
 *     ListNode next;
6
 *     ListNode(int x) {
7
 *         val = x;
8
 *         next = null;
9
 *     }
10
 * }
11
 */
12
public class Solution {
13
    public ListNode detectCycle(ListNode head) {
14
        if(head == null){
15
            return null;
16
        }
17
        ListNode fast=head,slow=head;
18
        while(fast != null){
19
            if(fast.next != null){
20
                fast = fast.next.next;
21
            }else{
22
                return null;
23
            }
24
            slow = slow.next;
25
            if(fast == slow){
26
                ListNode ptr = head;
27
                while(ptr != slow){
28
                    ptr = ptr.next;
29
                    slow = slow.next;
30
                }
31
                return ptr;
32
            }
33
        }
34
        return null;
35
    }
36
}

复杂度分析：

  • 时间复杂度：$O(N)$。
  • 空间复杂度：$O(1)$。